Encuentre el área de la región comprendida entre la parábola
Encontrar la parábola comprendida entre la siguiente integración.
2 Respuestas
Primero tienes que encontrar la intersección entre las dos curvas dato.
( x-5)^2 = x-3 ............la resolves y te esta dando x=7.
Por otro lado la parábola tiene por ordenada mínima x = 3 ( no esta definida para x<3 en campo real).
Area entre ambas = Integral ( f(x) - g(x)) dx entre X1= 3 Y x2= 7
http://www4f.wolframalpha.com/Calculate/MSP/MSP38601c5bc424g4f47b9600001ih1094a1158dea4?MSPStoreType=image/gif&s=57&w=272.&h=37.
Te participo de lo que yo estaría integrando:porque veo que no habia salido nada antes:
Por eso pongo los limites entre 3 y 7. Me refiero al área sombreada.
La integral no es difícil y a mi me daba 5.333 unidades de superficie.
;)
Hola Juan!
La contesté en el siguiente enlace: area parábola
Recuerda regresar aquí y votar a todos los expertos
Saludos
;)
;)
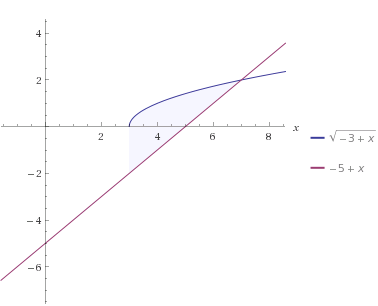
Creo que te equivocas al asumir que la intersección es de 3 a 7 , si resuelves la ecuación te da 2 soluciones x=7(como tu bien has dicho) y x=4, por tanto es desde ahí desde dónde tienes que integrar. Puedes comprobar mi respuesta y verás una aproximación de la gráfica de las funciones. - Kvothe Orwell
Bueno... pero yo me estoy refiriendo al área comprendida entre las dos... si integro. Desde x=4 me pierdo todo el área de la izquierda ( entre 3 y 4 )... lo que hice creo qué es lo que le están pidiendo a Juan... o me equivoco? - albert buscapolos Ing°
Es cierto , olvida el comentario anterior, sin embargo si integras respecto de x tienes que separar la parte de 3 a 4 porqué lo que estas integrando es la rama superior solamente, no se porqué pero ahora no se me carga la operación que has hecho, pero yo lo hice por 2 métodos diferentes y me dio lo mismo (9/2) así que creo que tu solución es incorrecta, si me he equivocado siento las molestias:) - Kvothe Orwell
Exacto, sin embargo estás contando área de más, te olvidas de la rama de la parábola que es negativa! , si ves mi respuesta verás a lo que me refiero. PD: como has introducido el gráfico ? , o es simplemente una imagen pegada? - Kvothe Orwell
Es imagen pegada. Esta en escala. Bueno esperemos a que Juan nos aclare cual le dan como solución .......................nos quedamos ambos en duda ....................sdos. - albert buscapolos Ing°
Esta claro que tu has calculado el área sombreada bien,en lo que no coincidimos es en que área es. La ecuación y^2=x-3 es una parábola con 2 ramas , y=sqrt(x-3) y y=-sqrt(x-3); Tu has cortado la curva por la mitad y has calculado ese área, pero no es el área entre las 2 curvas , es el área entre la recta y una nueva función que no es la del enunciado. Aún así , esperemos haber que respuesta le dan... - Kvothe Orwell