¿Cuál expresión que permite ver el desarrollo
El desarrollo de
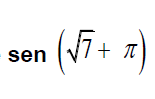
se se observa en la opción
$$\begin{align}& A=sen\ \sqrt{7 }\ \ \cos\ \ \pi\ + \cos\ \sqrt{7 }\ \ \ sen\ \ \pi \\\\& B=sen\ \sqrt{7 }\ \ \cos\ \ \pi\ -\ \cos\ \sqrt{7 }\ \ \ sen\ \ \pi \\\\& C=sen\ \sqrt{7 }\ \ \cos\ \ \sqrt{7 }\ \ +\ \cos\ \ \pi \ \ sen\ \ \pi \\\\& D=sen\ \sqrt{7 }\ \ \cos\ \ \sqrt{7 }\ \ - \cos\ \ \pi \ \ sen\ \ \pi \\\end{align}$$me hes de gran ayuda como siempre lo he mencionado.
2 Respuestas
Respuesta de albert buscapolos Ing°
1
Usas la identidad : sen ( V7 + pi) = sen V7 cos pi + cos V7 sen pi que corresponderia con la opcion A).
cOMPROBACION : sen ( V7 + 3.14 ) = sen (5.787) = -0.476
desarrollas la identidad ...sen V7. cos pi = - 0.476 ...............cos V7 sen pi = 0
Respuesta de javiabelo abelo
1
