Dos pequeñas esferas de masas respectivas
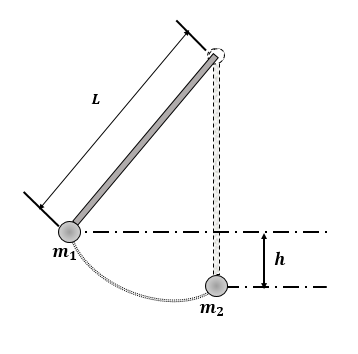
Dos pequeñas esferas, de masas respectivas m1 y m2 kg, cuelgan de un punto común mediante sendos hilos de longitud L m, como se indica en la figura 4. La esfera m2 se encuentra en reposo y la esfera m1 se abandona a partir de la posición que se indica, de modo que tenga lugar una colisión frontal y perfectamente elástica entre ambas esferas. Determinar la altura a la que ascenderá cada esfera después del primer choque.
DATOS
m1 (kg)2,20
m2 (kg)2*m1
L (m)0,512
Ayuda con procedimiento y solucion
¿Tienes la respuesta?
A mí me sale una repuesta en función de h.
Como es un choque elástico la Ep de m1 en el punto más bajo se habrá convertido en energía cinética Ek, la cual transfiere a m2, y ésta a la vez se hará energía potencial exclusivamente en el punto más alto de m2. Por lo tanto,
Ep1 = Ep2 Entonces m1gh1 = m2gh2 Pero como m2 = 2 m1 entonces
h2 = 1/2 h1
REspuesta la altura a la que sube m2 es la mitad de la altura en que se suelta m1.
Lo estaba desarrollando pero me dí cuenta que llegaba al mismo resultado, como dice Albertx, sin conocer h o el ángulo, yo tampoco llego a tener un número como respuesta.
Pongo el dibujo por si te sirve para algo, pero lo que he dicho arriba es válido
albert buscapolos Ing° Llaq Kmg Profesores no me da la profesora la información de (h) ya que precisamente de eso se trata el ejercicio de encontrar ese dato, el dice que hay que determinar la altura a la que ascenderá cada esfera
Si no te dan el ángulo de apertura ni la altura desde que se suelta m1, lo máximo que se consigue es que la altura a la que sube m2 es la mitad de altura de m1, en condiciones ideales. O al menos es lo máximo que yo he podido encontrar.
Si tu profesor te da la respuesta, por favor compártela, ya que yo también estoy aprendiendo.
1 respuesta más de otro experto
La masa m1 lanzada choca con la m2 en forma de choque elástico.
Velocidad de m1 al chocar = te saldria de........m1 g h = 1/2 m1vm11^2 ...........vm11^2=gh/0.5 =
Pero nos faltaría conocer h ( o el angulo de lanzamiento)... para seguir...