Calculo integral: Hallar el volumen del sólido generado al hacer girar en torno al eje y, la región en el primer cuadrante
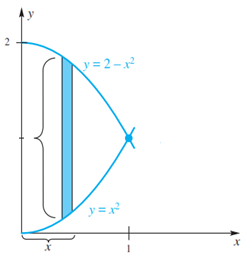
Hallar el volumen del sólido generado al hacer girar en torno al eje y, la región en el primer cuadrante que está por encima de la parábola y=x^2 y por debajo de la parábola y= 2-x^2 (ver figura). El volumen se expresa en unidades cúbicas.
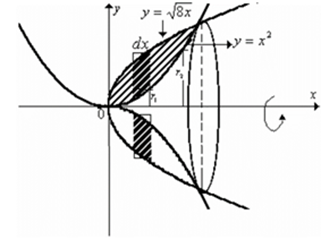
Hallar el volumen del solido que se genera al girar la región plana alrededor del eje x (ver figura). El volumen se expresa en unidades cúbicas.
1 Respuesta
Respuesta de Lucas m
2
;)
Hola jennifer!
Hacemos uno de esos por pregunta. Te hago el primero. Manda el otro en otra pregunta o espera a otro experto.
$$\begin{align}&V=2 \pi \int_a^b x([f(x)-g(x)]dx=\\&\\&2 \pi \int_0^1x(2-x^2-x^2)dx=\\&\\&2 \pi \int_0^12x-2x^3\ \ \ dx=\\&\\&2 \pi \Big [x^2- \frac{x^4} 2 \Big]_0^1=\\&\\&2 \pi(1-\frac 1 2)=\\&\\&2 \pi \frac 1 2=\\&\\&=\pi \ \ u^3\end{align}$$Saludos
;)
;)
Hola, gracias por la respuesta. Por favor, me podrías indicar las propiedades, definiciones o leyes utilizadas. Gracias de antemano. - María Rodríguez