Área de cara curva de un solido E

;)

Hola Carlos.

Si visualizas el sólido es lo que se denomina un huso esférico (la mitad z>0).

Como la traza es la recta

$$\begin{align}&y= \sqrt 3 \ x\\&\\&recta \ de \ pendiente \sqrt 3\ ==> forma \ un \ ángulo \ con \ las \ x \ positivas\\&de\ \alpha=arctan \sqrt 3=60º, luego\ con \ el \ plano \ x=0,eje Y==>30º\\&\\&Area\ huso= 4 \pi r^2\frac{ 30º}{360º}= \frac \pi 3\\&\\&Area_{solido}= \frac 12 \frac {\pi} 3= \frac {\pi}6\end{align}$$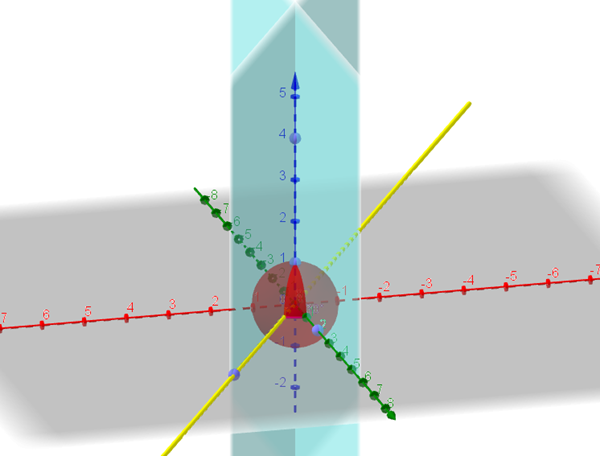

Eje X: :rojo

Eje Y : verde

Ejez: Azul

Recta (y plano) amarillo :

$$\begin{align}&y=\sqrt 3 x\end{align}$$

Con integrales de superficie,proyectando en el plano del piso XY:

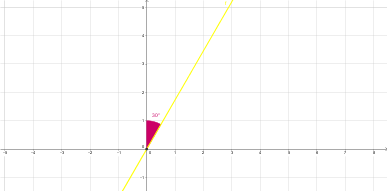
Esfera de radio 1:

$$\begin{align}&x^2+y^2+z^2=1\\&\\&z= \varphi(x,y)=\sqrt{1-x^2-y^2}\\&\\&dS= \sqrt{1+(\frac{\partial \varphi}{\partial x})^2+(\frac{\partial \varphi}{\partial y})^2}=\\&\\&\sqrt{1+\Big(\frac x{\sqrt{1-x^2-y^2}}\Big)^2+\Big(\frac y{\sqrt{1-x^2-y^2}}\Big)^2}\ \ dx\ dy=\\&\\&\sqrt{\frac{1-x^2-y^2+x^2+y^2}{1-x^2-y^2}}\ dx dy=\frac 1 {\sqrt{1-(x^2+y^2)}}\ dxdy\\&\\&A=\iint_{\varphi(A)}dS=\int_{x=0}^{x=1cos60º}\Bigg[\int_{ \sqrt 3 \ x}^{\sqrt{1-x^2}}\frac 1 {\sqrt{1-(x^2+y^2)}} dy \Bigg]dx=\\&a\ polares\ (Jacobiano=r))\\&\\&\int_{\frac{\pi} 3}^{\frac{\pi} 2} \Bigg [ \int_0^1 \frac 1{\sqrt{1-r^2}}·rdr \Bigg]d \theta=\\&\\&\int_{\frac{\pi} 3}^{\frac{\pi} 2} \Bigg [ \int_0^1 \frac 1{\sqrt{1-r^2}}·(-2r)\frac 1 2dr \Bigg]d \theta=\\&\\&\int_{\frac{\pi} 3}^{\frac{\pi} 2} \Bigg [ \int_0^1 \Big(1-r^2 \Big)^{-\frac 1 2}·(-2r)dr \Bigg]\frac 1 {(-2)}d \theta=\\&\\&\int_{\frac{\pi} 3}^{\frac{\pi} 2} \frac{\Big(1-r^2 \Big)^\frac 12} {\frac 1 2} \Bigg|_0^1 \frac 1 {-2} d \theta=\\&\\&\int_{\frac{\pi} 3}^{\frac{\pi} 2} \Big(1-r^2 \Big)^\frac 12 \Bigg |_0^1 (-d \theta)=\\&\\&\int_{\frac{\pi} 3}^{\frac{\pi} 2} \Big(1-1 \Big)^\frac 12-(1-0)\Big)(-d \theta)=\\&\\&\int_{\frac{\pi} 3}^{\frac{\pi} 2}d \theta= \frac {\pi} 2-\frac{\pi} 3=\frac {\pi} 6\end{align}$$

Saludos

;)

;)

;)