¿Como saber si la integral impropia es convergente o divergente?
Determinar si la integral impropia anterior es convergente o divergente.
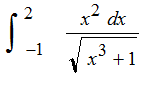
2 Respuestas
Respuesta de Mario Rodríguez
-1
Respuesta de Norberto Pesce
1

