Quien resuelve ejercicio de estática y resistencia

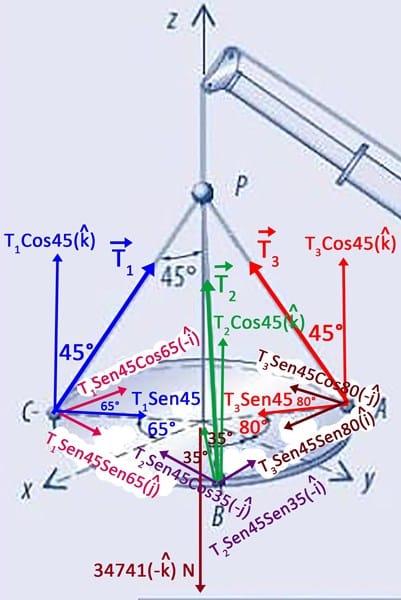
Primero hacemos un DCL tal como muestra la figura y por comodidad llamaremos CP=T1,

BP=T2 y AP=T3. También el vector PESO = W(-k) donde W=3545(9.,8)=34741N

descomponemos al vector T1 en sus dos componentes una vertical y otra radial :

T1Cos45(k) + T1sen45(r)

Descomponemos el vector radial en sus componentes X e Y:

T1sen45cos65(–i) +T1sen45sen65(j), entonces el vector T1 que da expresado en sus 3 componentes X, Y, Z tal como sigue:

– T1sen45cos65(i) + T1sen45sen65(j) + T1cos45(k)

Se hace lo mismo análogamente para los vectores T2 y T3 y obtenemos:

– T2sen45sen35(i) – T2sen45cos35(j) + T2cos45(k)

T3sen45sen80(i) – T3sen45cos80(j) + T3cos45(k)

Por condición de equilibrio T1+ T2 + T3 + PESO = 0

(–T1sen45cos65 – T2sen45sen35 + T3sen45sen80)(i) +

(T1sen45sen65 – T2sen45cos35 – T3sen45cos80)(j) +

(T1cos45 + T2cos45 + T3cos45 – 34741)(k) = 0

aplicamos a(i) + b(j) + c(k) = 0(vector), entoces a=0, b=0 y c=0

–T1sen45cos65 – T2sen45sen35 + T3sen45sen80 = 0 .........(1)

T1sen45sen65 – T2sen45cos35 – T3sen45cos80 = 0 ..........(2)

T1cos45 + T2cos45 + T3cos45 – 34741 = 0 .........................(3)

Tenemos 3 ecuaciones con 3 incógnitas (T1, T2, T3) el sistema si se puede resolver:

T1 = CP = 17 182.418 N

T2 = BP = 15 530.059 N

T3 = AP = 16 418.717 N