Transferencia de calor por convección

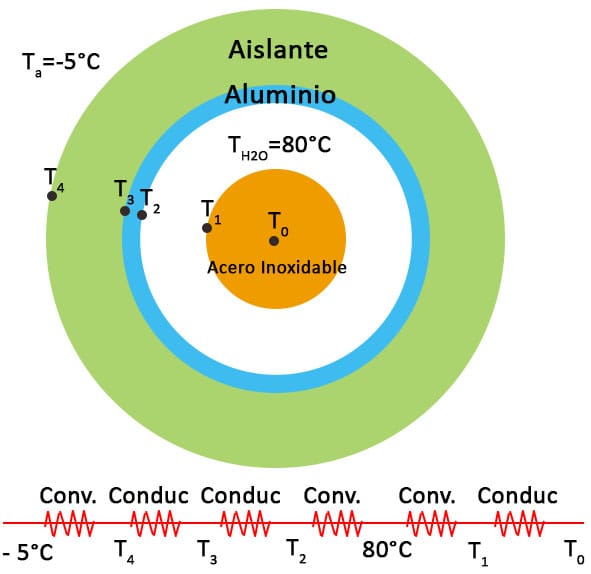
Q = ΔT/R,  donde R = Ln(r2/r1)/2πkL (Conducción)

                               R = 1/(hA) (Convección)

Resistencia Equivalente = Rconvec + Rconduc + Rconduc + Rconvec (desde -5°C hasta 80°C)

R_Equiv = 1/(h_e*2π*re_aislante*L) + Ln(re/ri)/(2π*k_aisl*L) + Ln(re/ri)/(2π*k_Al*L + 1/(h_agua*2π*ri_Al*L)

Tomando L=1m

R_Equiv =1/(20*2π*0.02) + Ln(0.02/0.014)/(2*PI*0.03) + Ln(0.014/0.013)/(2*PI*237) + 1/(150*2*π*0.013) =

R_Equiv = 0.3979 + 1.8922 + 4.98x10^-5 + 0.0816 = 2.3718 K/W

Q = [80-(-5)]/2.3718

Q = 35.8381 W (flujo constante)

Q = [T4 - (-5)]/Rconvec

QRconvec = T4 + 5

T4 = Q*Rconvec - 5 = 35.8381*0.3979- 5

T4 = 9.2595 °C

T3 =Q*Rcond + T4 = 35.8381*1.8922 +9.2595

T3 = 77.0732 °C

T2 = Q*Rcond +T3 = 35.8381*4.98x10^-5 + 77.0732

T2 = 77.0750 °C

T2 = 77.08°C

T_agua = Q*Rconvec + T2 =35.8381*0.0816 + 77.0750

T_agua = 80 °C

T1 = Q*Rconvec + 80°C  pero Rconvec = 1/(150*2*PI*0.006) = 0.1768

T1 = 35.8381*0.1768 + 80 = 86.3376

T1 = 86.34 °C

Para calcular T0 hacemos uso de la siguiente fórmula:

T0 = Flujo volumétrico de calor * R^2/(4k) + T1

T0 = Q*R^2/(4k*PI*R^2*L) + T1 para L=1m

T0 = Q/(4k*PI) + T1

T0= 35.8381/(4*15*PI) + 86.34 =86.5277

T0 = 86.53°C