2 respuestas
Es circuito mixto serie paralelo.
Deberias comenzar componiendo los paralelos AB y CD.
Paralelo AB = 1/ (1/16 + 1/32) = 1 / (0.0625 + 0.03125) = 1/ 0.09375 = 10.67 ohms
Paralelo CD= 7.5 ohms. Es fácil porque ambas resistencias son iguales.
Y Luego tendrías la Resistencia equivalente que ve la fuente:
Requ. = 10.67 // ( 8.50 + 7.50) = 10.67 // 16 = 1 / ( 1/10.67 + 1/16) = 1 / ( 0.0937 + 0.0625) = 1 / 0.1562 = 6.40 ohms.,,,seria la resistencia que ve la fuente.
La corriente que entrega será = 38.4 V / 6.40 ohms = 6 A,
La intensidad de la corriente en los resistores de 32 y 8.50 ohms te lo dejo a vos. Es muy fácil planteando Ley de ohm en cada rama.
La potencia disipada, con las corrientes del párrafo anterior, la hallas inmediatamente mediante W = I^2 R.
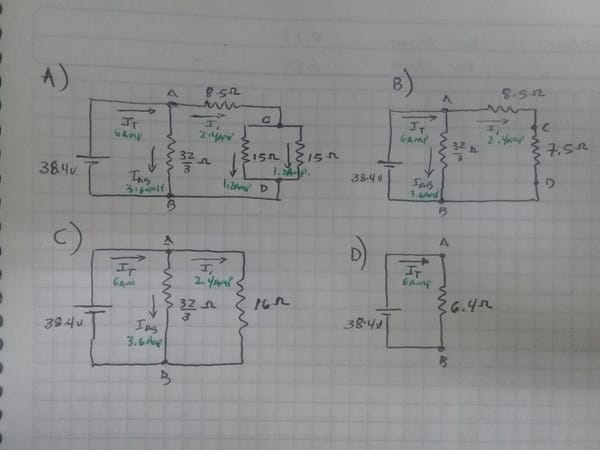
a) La resistencia total la encuentras con las fórmulas que ya debes saber de resiatencias en serie y en paralelo.
Hace falta observar. Entre los nodos "A" y "B", claramente en paralelo las resiatencias de 16 y 32 ohms.
Entonces la resistencia equivalente en este circuito es:
$$\begin{align}&R_{AB}=\frac {1}{\frac {1}{16}+\frac {1}{32}}= \frac {32}{3}{\Omega}\\&\end{align}$$Ahora, redibujas el circuito como el circuito A) de la figura.
Entre los puntos "C" y "D", las resistencias de 15 ohms están en paralelo, por lo que utilizas la misma fórmula para obtener la resistencia equivalente y redibujas el circuito como el circuito B).
Se observa claramente que las resistencias de 2.4 ohms y la resistencia calculada, están en serie, así que sus valores se suman y se redibuja el circuito C). Donde se observa claramente que las resistencias están en paralelo, así que aplicas la fórmula para resistencias en paralelo y redibujas el circuito como D).
b) Aquí ya es muy fácil utilizar la ley de ohm para encontrar la corriente máxima que va a entregar la fuente de 38.4V. [V=I×R]=6 Amp.
c) La corriente en la resistencia de 32 ohms la calculas también con la ley de Ohm, ya que se observa que el voltaje entre "A" y "B" es el mismo de la fuente, así que la corriente te va a dar 1.2 Amp.
Para calcular la corriente en la resistencia de 8.5 ohms, tienes que calcular la corriente en la resistencia equivalente "AB", y luego se la restas a la corriente total, el resultado es la corriente que vamos a llamar I1, que circula por la resistencia de 8.5 ohms.
d) La potencia disipada en una resistencia la calculas: P=V×I . Como ya sabes cuanta corriente circula en cada resistencia, puedes facilmente encontrar que en la R=32ohms, la potencia es de: P=38.4V×1.2=46.08 Watts.
Para la resistencia de 8.5 ohms, podemos calcular su potencia, si primero calculamos el voltaje en ella utilizando la ley de Ohm o bien utilizando la fórmula:
$$\begin{align}&P=I^2×R=48.96 W\end{align}$$Que se deduce fácilmente de la formula V=I×R
