Ejercicio de física de movimiento oscilatorio
Ejercicio (Movimiento oscilatorio)
Tenemos un muelle ideal de longitud l0=40 cm. Cuando colgamos un objeto de masa m=2 kg, se observa que el muelle se estira 10 cm.
- a) Encuentre el período y la frecuencia del muelle.
- b) Si la estiramos 15 cm y la soltamos, ¿qué velocidad tendrá cuando pase por la posición de equilibrio? ¿Cuánto vale la aceleración en ese instante?
- c) ¿Cuánto vale la aceleración del objeto al encontrarse 2,5 cm por encima de la posición de equilibrio?
- d) ¿Cuánto tiempo pasa entre que el objeto pasa de estar 2,5 cm por debajo de la posición de equilibrio a estar 2,5 cm por encima de la posición de equilibrio?
1 Respuesta
Comenzá haciendo el croquis del sistema. Eje y . Masa de 2 Kg. colgada del mismo.
Elongación inicial : longitud en reposo del muelle + estiramiento por la fuerza peso.
Elongación inicial = - 0.40 - 0.10 = - 0.50 m. Valores medidos desde el punto de suspensión del resorte.
La tomamos como referencia del movimiento oscilatorio. Alrededor de ese valor oscilará la masa.
Si te dicen que con ese peso se estira 0.10 m .luego K = 20 N / 0.1 m = 200 N/m.
- a) T = PERIODO = 2pi V(m/K)= 2PI V( 1/100) = pi/5 s.
F= FRECUENCIA = 1/T = 5/pi s^-1
Ademas calculas la pulsacion w= 2 pi f = 2 pi x 5/pi = 10 /s.
- b) La función que te representa este movimiento, comenzando desde 0.15 m abajo ( -0.15 m) sera una cosinusoide de amplitud =/ 0.50 +/- 0.15/
Para analizarla más fácilmente te reflejando las condiciones iniciales, te conviene expresarla así::.
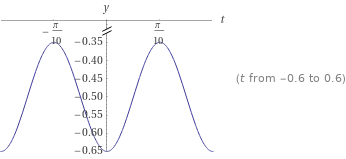
y(t) = - 0.50 + 0.15 cos ( wt + pi) = - 0.50 + 0.15 cos ( 10 t + pi) .
Derivando obtenes:
Velocidad: dy/dt = - 0.50 x10 sen (10t + pi)= - 5 sen (10t + pi)
Aceleracion : dv/dt = - 50 cos ( 10 t + pi)
Para la primera posicion de equilibrio t= pi/20 y allí se dan:
Velocidad = v(t) = -0.50 sen ( 10. pi/20 + pi ) = - 6.50 x -1= 5 m/s ( hacia arriba y será la maxima)
Aceleracion = -50 cos ( 10. pi/20 + pi ) = 0 m/s^2 ..Aceleracion nula.
- c) Si la masa se encuentra 0.025 pasando por la primera posicion de equilibrio, tendras que calcular el T1 correspondiente para y = -0.50+0.025= -0.475 m.
- 0.475 = -0.50 + 0.15 cos ( 10 T1 + pi) ..................y de aqui despejas T1.
Ese valor de T1, lo llevas a la expresión de la aceleración y obtenés lo que te piden.
- d) Muy aproximadamente este tiempo = 2T1
Te paso el gráfico de la respuesta del sistema como función del tiempo:
Posicion de equilibrio será yo = - 0.50 m.
