Preguntas esperando respuesta
Actividad pública reciente
Ha preguntado en el tema en
Matemáticas
y en 1 temas más
El contorno de una lámina delgada es una elipse de semi-ejes a y b.
Al que por favor me pueda colaborar con este ejercicio. Muchas gracias El contorno de una lámina delgada es una elipse de semi-ejes a y b. L representa una recta en el plano de la lámina que pasa por el centro de la elipse y forma un ángulo α con el...
Sin respuestas
Ha preguntado en el tema en
Matemáticas
y en 1 temas más
Una lámina delgada de densidad constante K está limitada por dos circunferencias concéntricas
Alguien podría colaborarme con este ejercicio. Muchas gracias. Una lámina delgada de densidad constante K está limitada por dos circunferencias concéntricas de radios a y b y centro en el origen, siendo 0<b<a, calcule el momento Io.
Sin respuestas
Ha empezado a seguir a 
antoniomallo
antoniomallo
Ha valorado "Excelente" la respuesta
Un tanque de 500 galones contiene inicialmente 300 galones de solución salina en la que se han disuelto 50 libras de sal.
Iniciamente hay en el tanque 50 libras de sal. En el momento en que se desborda han entrado en el tanque 500 - 300 = 200 galones, conteniendo 200 galones · 3 libras / galón = 600 libras de sal, que sumadas a las 50 libras que había hacen un total de...
Ha preguntado en el tema en
Matemáticas
y en 1 temas más
Suponga que un cuarto contiene 32m^3 de aire, originalmente libres de monóxido de carbono.
Alguien que por favor me pueda ayudar con este ejercicio. Suponga que un cuarto contiene 32m^3 de aire, originalmente libres de monóxido de carbono. En el instante t = 0 se empieza a introducir al cuarto humo de cigarrillo, con un contenido del 4% de...
Sin respuestas
Ha preguntado en el tema en
Matemáticas
y en 1 temas más
Utilice la transformada de Laplace para resolver la ecuación:
El siguiente ejercicio me dice: Utilizar la transformada de Laplace para resolver la siguiente ecuación.
Sin respuestas
Ha valorado "Excelente" la respuesta
Halle las ecuaciones simétricas de la recta tangente a la curva
· · ¡Hola Jhon! Lo que debemos hacer es calcular la intersección en forma de curva paramétrica, entonces es muy fácil calcular el vector derivada y la recta que pasa por ese punto. Y eso es todo, saludos. : :
Ha valorado "Excelente" la respuesta
Hallar la segunda derivada de la siguiente función: ∂z/∂r = Fx*cosΘ + Fy*senΘ
· · ¡Hola Jhon! No entiendo muy bien lo que quieren decir, a lo mejor necesitaría saber el enunciado completo o el contexto del ejercicio. Veamos lo que pieso Z es una función de r y theta Pero a su vez r y theta son funciones de x y y. Y si es como...
Voto positivo a la respuesta
Hallar la ecuacion de la recta , que pasa por el punto (3,4), determina en el primer cuadrante con los ejes coordernados;un tria
· · ¡Hola José! Las rectas que pasan por (3,4) son y-4 = m(x-3) Si el corte con el eje X es (a, 0) 0-4 = m(a-3) m= -4/(a-3) entonces el corte con el eje Y será y - 4 = [-4/(a-3)](0-3) y = 4 +12/(a-3) este será el corte (0, 4 + 12/(a-3)) Y el área del...
Ha valorado "Excelente" la respuesta
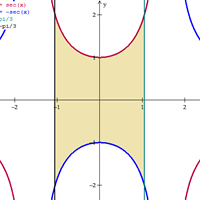
Determine el volumen del sólido acotado por el frente y por detrás por los planos x=pi/3, a los lados por los cilindros
· ¡Hola Jhon! Imagino que quieres decir los planos x=-pi/3 y x=+pi/3, así sí que se define una región en el plano z=0 que será el dominio de integración. Y esto yo no se si lo hacéis como integral doble o triple, sabes que es lo mismo, si lo haces...
Ha valorado "Excelente" la respuesta
Demuestre que el producto de los senos de los ángulos de un triángulo alcanza su mayor valor cuando.
· · ¡Hola Jhon! Podemos tomar dos ángulos siempre que estén en el intervalo (0, pi) y la suma de los dos también esté en ese intervalo. El tercer angulo queda determinado por los dos primeros y por lo tanto su seno también. Entonces el producto de...
