Determine el volumen del sólido acotado por el frente y por detrás por los planos x=pi/3, a los lados por los cilindros

$$\begin{align}& \end{align}$$

·

¡Hola Jhon!

Imagino que quieres decir los planos x=-pi/3  y  x=+pi/3, así sí que se define una región en el plano z=0 que será el dominio de integración.

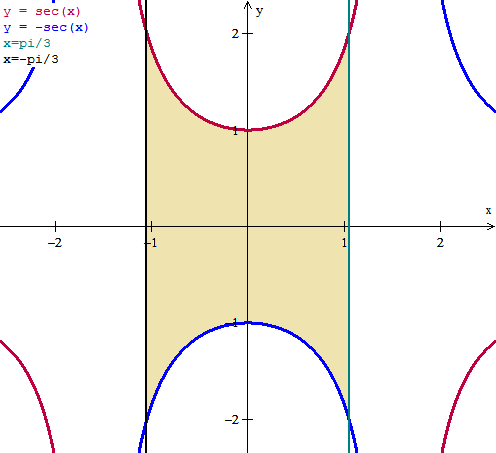
Y esto yo no se si lo hacéis como integral doble o triple, sabes que es lo mismo, si lo haces como triple en el primer paso llegas a la doble. Y como es un paso tan sencillo empezaré en la doble.

$$\begin{align}&A=\int_{-\pi/3}^{\pi/3}\int_{-sec\,x}^{sec\,x}(1+y^2)dy dx=\\&\\&\int_{-\pi/3}^{\pi/3}\left[y+ \frac{y^3}{3}  \right]_{-sec\,x}^{sec\,x} dx=\\&\\&\int_{-\pi/3}^{\pi/3} \left(sec\,x + \frac{sec^3x}{3}+sec\,x+\frac{sec^3 x}{3} \right)dx=\\&\\&2\int_{-\pi/3}^{\pi/3}\left(sec\,x+\frac{sec^3x}{3}\right)dx\end{align}$$

¡Será posible!  Pues si ya saben cómo me pongo ¿para qué ponen integrales de secantes? ¡Ja Ja!

Odio las integrales de las secantes, no son inmediatas y son muy difíciles. Si en algún sitio aparecen como inmediatas te están engañando.

Aquí te dejo los enlaces donde he hecho estas integrales y te dejo que lo termines tú.

¿Cómo resolver la integral? Con procedimiento ¿Cómo resolver la integral? Con procedimiento

¡Ah pues yo pensaba que tenía hechas las dos pero la de la secante al cubo no la encuentro!

Por favor, manda una pregunta nueva con la integral de la secante al cubo e intentaré hacerla. ¡Que vaya ejercicio os han clavado!

Saludos.

:

.