Duda sobre fiabilidad en estadistica
Me ha surgido una duda a mitad de la resolución de este problema:
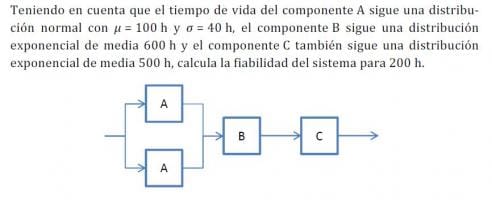
Yo primero calculo la probabilidad en paralelo de los dos A y me sale 0.0123
Para seguir se supone que tendría que multiplicar el resultado antes mencionado por P(B) y luego por P(C) ya que los tres están en serie.
Como P(B) y P(C) las calculo para una fiabilidad de 200 horas que es inferior a su media de cada una, yo tengo que suponer : P(B) = P(C) =1 = 100% de fiabilidad ??
Gracias por la ayuda.
1 respuesta
Respuesta de Valero Angel Serrano Mercadal
1

