Encuentra la ecuación y la gráfica de la cónica con excentricidad y cuyos vértices coordenados

La excentricidad es el cociente entre la distancia focal y la longitud de eje principal. Dichas distancias son 2c y 2a, luego la excentricidad es

e=c/a

En las elipses c^2 = a^2 - b^2 y los valores da la excentricidad son 0 <= e <1

En la parábola e=1

En las hipérbolas c^2 = a^2+b^2 y la excentricidad es 1< e < oo

Como la que nos dan es

e = 4/5 < 1 la cónica es una elipse.

Siendo los vértices (-2, 7) y (8,7) la longitud del eje es 8 -(-2) = 10, luego a=5 y tendremos

e = c / a = c/5 = 4/5

luego c=4

c^2 = a^2 -b^2 = 25 - b^2 = 16

b^2 = 25-16 = 9

b=3

Luego ya conocemos

a=5 y b=3

Además podemos calcular el centro de la elipse ya que está a distancia 5 de los vértices, por lo tanto en x es -2+5 = 3 y el centro es (3, 7)

Con estos datos la ecuación canónica de la elipse es:

$$\begin{align}&\frac{(x-3)^2}{5^2}+\frac{(y-7)^2}{3^2}=1\\ &\\ &\text{si queremos la ecuación general será}\\ &\\ &9(x-3)^2+25(y-7)^2=225\\ &\\ &9x^2-54x +81+25y^2-350y+1225=225\\ &\\ &9x^2+25y^2-54x-350y+1081=0\end{align}$$

Y esta es la gráfica de la cónica.

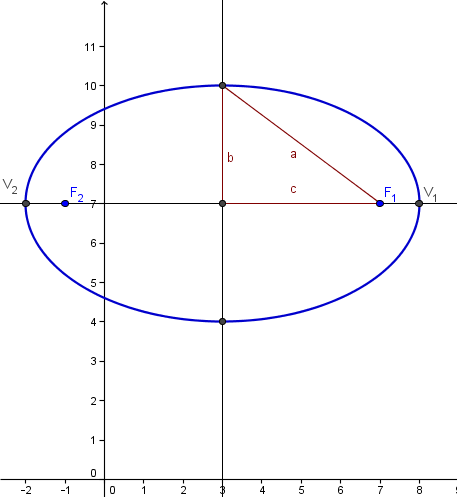
Y esto ya es bastante trabajo para una pregunta. La parte de Brianchon podría ser tranquilamente otra pregunta. Además para el teorema de Brainchon se necesitan seis puntos y solo me proporcionas dos. Y aparte ya hice un problema similar a este (o este mismo) y me juré que no debía hacer otro. Aquí te dejo los enlaces.

Primera parte

Lamentablemente la segunda parte no se localiza, en TodoExpertos pierden o eliminan algunas respuestas. Y aun queda mucho trabajo y como te dije juré no volver a hacerlo.