Dibujar una función

Ya no me acuerdo cuáles eran todas las cosas que se pedían en estos ejercicios. Mejor me cojo el libro para no olvidarme ninguna.
1) Dominio de la función:
Esta definida para todos los valores reales excepto para x=1
Dom f = (-infinito, 1) U (1,+infinito)
2) Ceros de la función.
Son los valores que anulkan el numerador
x^2 - 3x - 5 = 0
x = [3 +- sqrt(9 +20)] / 2 = (3 +- sqrt(29)) / 2
Aproximadamente x1 = -1,1925824 y x2 = 4,1925284
3) Continuidad. Es continua para todos los valores salvo x = 1
4) Signos Los únicos puntos donde puede cambiar el signo es en los ceros y en punto de discontinuidad
En (-infinito, -1,1925384) tomemos f(-2) =5/(-3) < 0 es negativa
en (-1,1925384, 1) tomemos f(0) = -5/(-1) = 5 >0 es positiva
en (1, 4,1925284) tomemos f (2) = -7/1 < 0 es negativa
en (4,1925284, +infinito tomemos f(5) = 5/4 >0 es positiva
5) Simetrías. No las tiene.
6) Periodicidad. No es periódica.
7) Asíntotas.
a) Verticales en x= 1. A la izquierda tiende a +infinito y a la derecha a -infinito.
b) Horizontales. Para x tendiendo a infinito también la y, luego no hay
c) Oblicuas.
m = lim x--> infinito f(x)/x = lim (x^2-3x-5)/[x(x-1)] = 1
n = lim x --> infinito (fx) - mx = lim (x^2-3x-5 -x^2+x)/(x-1)= -2
La asíntota es la recta y = x - 2
8) Intersecciones con lo ejes.
Los ya referidos (-1,1925824, 0) y (4,1925284, 0) con el eje X
y con el eje Y el punto (0,5)
9) Crecimiento, máximos y mínimos.
f'(x) = [(2x-3)(x-1) - (x^2-3x-5)] / (x-1)^2 = (2x^2 - 2x -3x +3 -x^2 +3x + 5)/(x-1)^2 =
(x^2 - 2x + 8 ) / (x-1)^2
El discriminante del numerador b^2 - 4ac = 4 -32 = -24 es negativo, luego la ecuación del numerador no tiene ceros y es siempre positic¡Va. Y el denominador siempre positivo también.
Luego la derivada es siempre positiva donde existe y la función es siempre creciente.
No tiene máximos o mínimos relativos.
10) Puntos de inflexión, concavidad, convexidad.
No tiene puntos de inflexión al no anularse nunca la derivada primera.
f''(x) = (2x-2)(x-1)^2 - 2(x-1)(x^2 -2x +8) / (x-1)^4 =
[(2x-2)(x-1) - 2(x^2 - 2x +8)] / (x-1)^3 = -14/(x-1)^3
f''(x) = -14/(x-1)^3
Esto depende del signo del denominador que será negativo hasta x=1 y positivo después
En (-infinito, 1) f''(x) > 0 la función es cóncava.
En (1,+infinito) f''(x) < 0 la función es convexa.
Creo que esas son todas las cosas que piden. Y ya está bien porque es un oficio en extinción, con los ordenadores no cuesta nada hacer las gráficas. Ya no hace falta realizar estos estudios tan ingratos.


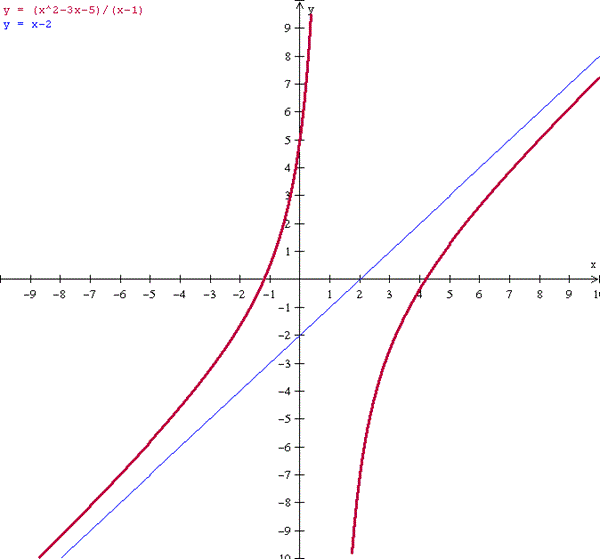
Y con esto creo que está todo hecho. Mira a ver que tal lo habías hecho tu. No olvides puntuar para cerrar la pregunta.