Ejercicio integración de calculo 3

Dianis 1556!
Haremos primero la gráfica del dominio para comprender mejor el problema. Las ecuaciones de las rectas se sacan por la fórmula de que la recta que pasa por (x1, y1) (x2, y2) tiene ecuación (x-x1) / (x2-x1) = (y-y1) / (y2-y1). Si a ti no te gusta puedes hacerlo que tu forma favorita que hay muchas.

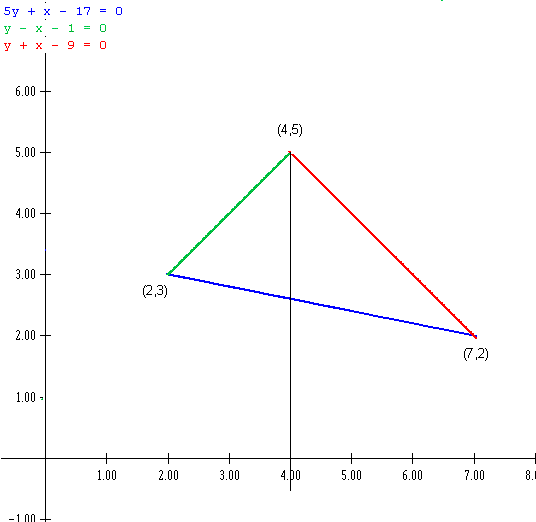
Dividiremos el dominio en dos partes por la recta negra que he trazado, así tendremos estos dos dominios:
x € [2,4]; y € [x+1, (17- x)/5]
x€ [4,7]; y € [x+1, 9-x]
$${2xdy en y € [x+1,(17-x)/5]}dx en x€[2,4] + $${2xdy en y € [x+1,9-x]}dx en x€[4,7]=
${2xy en y € [x+1,(17-x)/5]}dx en x€[2,4] + $${2xy en y € [x+1,9-x]}dx en x€[4,7] =
${2x(17-x)/5 - 2x(x+1)}dx en x€[2,4] + ${2x(9-x) -2x(x+1)}dx en x€[4,7]=
${34x/5 - 2(x^2)/5 - 2x^2 - 2x}dx en x€[2,4] + ${18x-2x^2-2x^2-2x}dx en x€[4,7]=
${(24/5)x - (12/5)x^2}dx en x€[2,4] + ${16x - 4x^2}dx en x€[4,7]=
[(12/5)x^2 - (4/5)x^3] en x€[2,4] + [8x^2 - (4/3)x^3] en x€[4,7] =
(12/5)·16 - (4/5)·64 -(12/5)·4 + (4/5)·8 + 8·49 - (4/3)·343 - 8·16 + (4/3)·64 =
12(12/5) - 56(4/5) - 279(4/3) + 264 = 144/5 - 224/5 - 1116/3 + 264 = ...
Estas cuentas me van a matar, es inhumano. Esta vez estoy convencido que están mal. Repasa lo que quieras pero yo me planto aquí.
No olvides puntuar por favor, que vaya cabeza llevo!

Espera, déjala abierta de momento. Cuando tenga tiempo y la cabeza bien despejada miraré a ver donde está el fallo. Estoy seguro que debe haberlo porque la integral me salía negativa cuando la función 2x era positiva en todo el dominio.
Pero ahora tengo que hacer mis cosas normales, dentro de unas seis horas puede que me ponga a revisarlo.

Pues el fallo está al principio en la definición del dominio que está mal, con lo que hay que calcular todo de nuevo.
Dividiremos el dominio en dos partes por la recta negra que he trazado, así tendremos estos dos dominios:
x € [2,4]; y € [(17- x)/5, x+1] Este estaba al revés
x€ [4,7]; y € [(17-x)/5, 9-x] En este la primera recta era otra.
$${2xdy en y€[(17-x)/5,x+1]}dx en x€[2,4] + $${2xdy en y€[(17-x)/5,9-x]}dx en x€[4,7]=
${2xy en y€[(17-x)/5,x+1]}dx en x€[2,4] + ${2xy en y€[(17-x)/5,9-x]}dx en x€[4,7] =
${2x[x+1-(17-x)/5]}dx en x€[2,4] + ${2x[9-x-(17-x)/5}dx en x€[4,7] =
${2x[x+1-(17/5)+x/5]}dx en x€[2,4] + ${2x[9-x-17/5+x/5]}dx en x€[4,7] =
${2x[(6/5)x-(12/5)}dx en x€[2,4] + ${2x[28/5 -(4/5)x]}dx en x€[4,7] =
${(12/5)x^2 - (24/5)x}dx en x€[2,4] + ${(56/5)x - (8/5)x^2}dx en x€[4,7] =
[(4/5)x^3 - (12/5)x^2] en x€[2,4] + [(28/5)x^2 - (8/15)x^3] en x€[4,7] =
(4/5)64 - (12/5)16 - (4/5)8 + (12/5)4 +(28/5)49 - (8/15)343 - (28/5)16 + (8/15)64 =
56(4/5) - 12(12/5) +33(28/5) - 279(8/15) = (224 - 144 + 924 - 744) / 5 =
260 / 5 = 52
Y eso es todo, ahora creo que está ya bien y espero que lo hallas entendido. NO olvides puntuar.