Dianis 1556!
Es imprescindible el gráfico para entender la complejidad del problema.
Aunque previamente calculamos los puntos de intersección de ambas circunferencias.
De x^2 + (y-2)^2 = 2
(y-2)^2 = 2 - x^2
Como tomamos la parte de abajo
y-2 = -sqrt(2-x^2)
y = 2 - sqrt(2-x^2)
De x^2 + y^2 = 4
y = sqrt(4-x^2)
Luego:
2 - sqrt(2-x^2) = sqrt(4-x^2)
4 + 2 - x^2 - 4 sqrt(2-x^2) = 4 - x^2
2 - 4 sqrt(2-x^2) = 0
4sqrt(2-x^2) = 2
16(2-x^2) = 4
2 - x^2 = 1/4
x^2 = 2 - 1/4 = 7 / 4
x = +- sqrt(7)/2y = sqrt(4-x^2) = sqrt(4-7/4) = sqrt(9/4) =
3/2Los puntos de intersección son (-sqrt(7)/2, 3/2) y (sqrt(7)/2, 3/2)
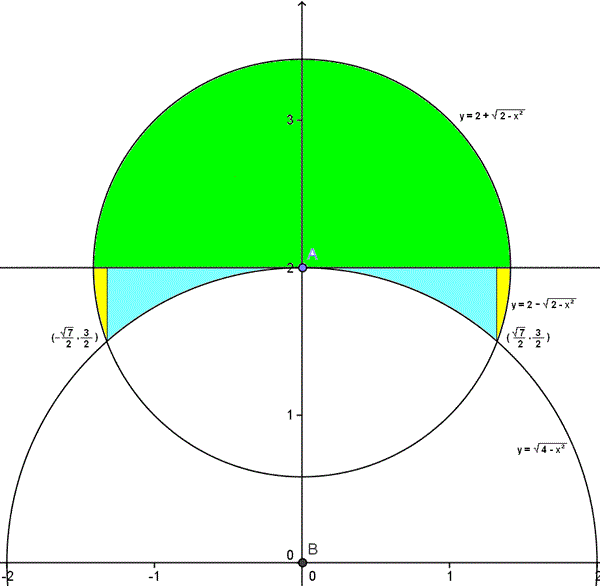
Toda la zona coloreada es el área que nos piden.
La parte verde no es necesario integrarla
Área verde = (1/2)PI[sqrt(2)]^2 = PI
Area amarilla = |2 $$dydx en x€[sqrt(7)/2, sqrt(2)]; y€[2-sqrt(2-x^2), 2]|
Area azul =|2 $$dydx en x€[0, sqrt(7)/2]; y€[sqrt(4-x^2), 2]|
Calculemos
Área Amarilla. Tras la integración respecto a y que da y, su sustitución y simplificación queda
Area amarilla = 2 |$sqrt(2-x^2)dx en x€[sqrt(7)/2, sqrt(2)]|
Hagamos la integral indefinida con el cambio
x = sqrt(2)seny
dx = sqrt(2)cosy·dy
$sqrt(2-x^2)dx = $sqrt(2-2sen^2(y))·sqrt(2)cosydy = 2$cos^2(y)dy =
Usamos la fórmula trigonométrica cos^2(a) = [1 +cos(2a)]/2
= $(1+cos(2y) dy = y + (1/2)sen2y =
Deshaciendo el cambio
= arcsen(x/sqrt(2)) + sen(2arcsen(x/sqrt(2))) =
El seno del doble de un ángulo a es 2·sena·cosa. En nuestro caso conocemos sena=x/sqrt(2) y por ende cosa=sqrt(1-sen^2(a) = sqrt[1-(x^2)/2]. Luego
2cosasena=2(x/sqrt(2))(sqrt[1-(x^2)/2] =(x·sqrt (2-x^2))/2
Bueno, recapitulamos:
$sqrt(2-x^2)dx = arcsen(x/sqrt(2)) + (x·sqrt (2-x^2))/2
Ahora calculamos la definida en el intervalo [sqrt(7)/2, sqrt(2)] =
arcsen(1) + sqrt(2)sqrt(0)/2 - arcsen([sqrt(7)/2]/sqrt(2)) - (1/2)[sqrt(7)/2]sqrt(2-7/4)=
PI/2 - arcsen(sqrt(7/8)) - sqrt(7)/8 = 1,5707963 - 1,2094292 - 0,3307189 = 0,0306481
Area amarilla = 2 |0,0306481| = 0,0612963
¡Qué lio me he montado! No puedo seguir se mue hizo muy tarde, ya lo terminaré, aun falta calcular el área azul.




