Bueno el problema a queda así entonces, calcular el volumen de la región del espacio delimitida por el plano z=0 como base, el plano z= y como altura y el cilindro x^2+y^2=4 como pared lateral. Creo que es bastante sencilllo de intuir.
El plano z=y será negativo cuando y sea negativo y no será el techo sino lo contrario, luego solo debemos integrar cuando la y sea positiva.
El dominio de integración es por tanto medio circulo con x€[-2, 2] e y€[0,sqrt(4-x^2)]
V$${ydy en y€[0,sqrt(4-x^2)]}dx en x€[-2,2] =
${(y^2)/2 en y€[0,sqrt(4-x^2)]}dx en x€[-2,2]=
$ (4-x^2)/2 dx en x€[-2,2] =
2x - (1/6)x^3 en x€[-2,2] =
4 - 8/6 +4 - 8/6 = 8 - 16/6 = (48-16)/6 = 32/6 =
16/3-------------------
b) En este haremos el dibujo que es menos claro
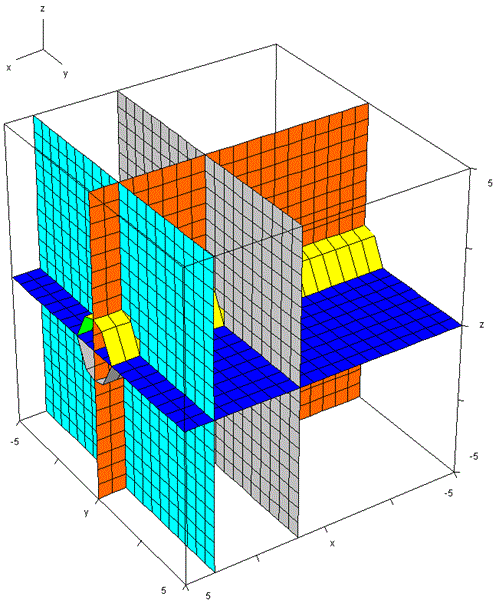
En este caso es el cilindro caso el que hace de techo. Pero como nos dicen que la integral sea triple tendremos que expresarlo como dominio en lugar de hacer una doble y ponerlo como función a integrar.
Los límites son bien claros:
En x€[1,4]
En y entre el cero y el radio del cilindro luego y€[0,1]
En z la altura desde 0 hasta el valor de la función cilindro que depende de y. Luego z€[0,sqrt(1-y^2)]
Y la función a integrar es la identidad porque el dominio ya contiene las tres dimensiones
$$$dz en z€[0,sqrt(1-y^2)] dy en y€[0,1] dx en x€[1,4]
$${sqrt(1-y^2)dy en y€[0,1]}dx en x€[1,4]
Ya hicimos ayer dos integrales de este tipo, además sabemos que eso no es otra cosa que la cuarta parte del circulo de radio 1 luego la integral más interna vale PI/4
$PI/4dx en x€[1,4] = PI/4 · x en [1,4] = PI - PI/4 =
(3/4)PIY eso es todo.


