Roca 73 2!
a) f(x,y) = x^2 ln( y^2 - x)
El dominio se restringe a los puntos donde y^2 -x > 0 porque el logaritmo neperiano solo está definido para esos puntos.
Luego
y^2 - x >0
y^2 > x
Dom f = {(x,y) € RxR | y^2 > x}
Si usamos la igualdad tenemos y^2=x tenemos una parábola simétrica en el eje X con vértice en (0,0) y con dirección a +infinito.

La parábola divide al plano en dos zonas. La que verifica y^2 > x que es la que nos interesa y la otra.
Para saber cuál es cuál tomemos un punto cualquiera y veamos qué desigualdad verifica.
Tomamos el punto (1,0) que es interior, tendremos
y2=0; x=1
Luego y2 < x que es lo contrario de lo que nos piden.
La zona que cumple es la que hay fuera de la parábola.
------------------
b) f(x,y) = [(1+x-y)^1/2] / (x-1)
El dominio esta limitado a los puntos donde
1+x+y >= 0 porque la raíz solo esta definida para numeros >= 0
Además los puntos de la recta x=1 tampoco pertenecen al dominio porque se anula el denominador.
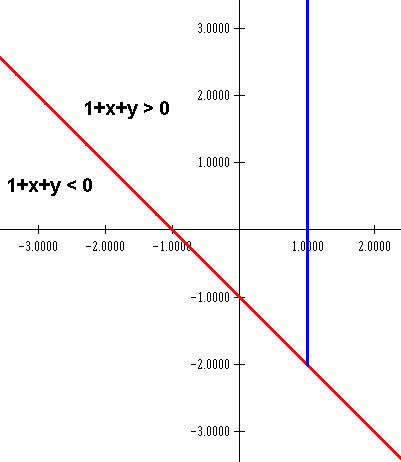
La recta 1+x+y = 0 divide el plano en dos zonas. Una con >=0 y otra con <0
Probamos el punto (0,0) por ejemplo que está en la parte superior
1+0+0 >= 0
Es lo que necesitamos, luego el dominio es la parte superior y la recta incluida, del cual habrá que descontar la recta pintada en azul porque hace cero el denominador.
Dom f ={(x,y) €RxR | 1+x+y >= 0; x <> 1}
El <> es el signo distinto en computación.
Y eso es todo, espero que te sirva y lo hallas entendido. NO olvides puntuar.


