Encontrar razón de dos lados en triángulos
Hola! Ojalá me puedas ayudar con el siguiente ejercicio de geometría.
Sea ABC un triángulo rectángulo con ángulo recto en B. Sea D un punto tal que BD es perpendicular a AC y DC = AC. Encuentra AD/AB.
Gracias.
1 respuesta
Laa preguntas de geometría pueden ser muy complicadas porque no hay una geometría, hay muchas. Y si se salen un poco de lo común hay que saber que es lo que se está estudiando. Para hacerlo bien sería necesario haber ido a la misma clase que tú, con los mismos libros y todo. No se si me podrás decir de que va lo que estáis estudiando, algún teorema, el libro si lleváis o algo que me ayude. Yo lo estoy intentando con métodos más bien geométricos pero no me sale nada, creo que tendré que echar mano de ecuaciones de rectas, circunferencias y ese tipo de geometría a no ser que me digas algo.
Hola! solo nos comentó el maestro que usáramos la semejanza y la propiedad de la altura.
Ahora tengo que ir a dormir. No sé si lo tengo ya pero no me da tiempo a explicarlo. De todas formas desde el primer día sé que la respuesta es raíz de 2, lo complicado es demostrarlo. Pero por si te sirve esa es la repuesta. Espera a ver si logro demostrarlo.
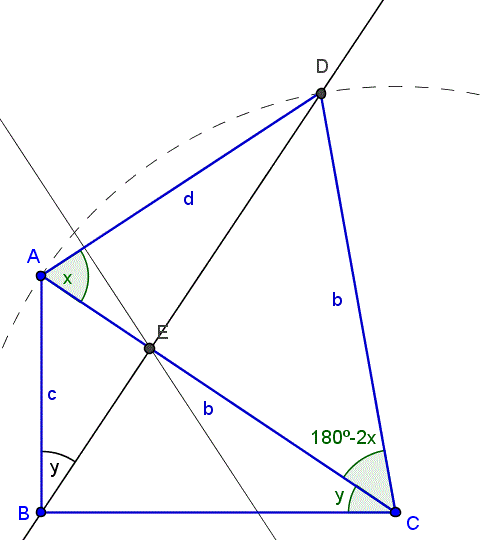
Podemos definir el triángulo ABC mediante el lado c y el ángulo que he llamado y.
Vamos a calcular d de dos formas y así tendremos dos ecuaciones donde despejar x y d.
$$\begin{align}&d=\frac{\overline{AE}}{cosx}= \frac{c·seny}{cosx}\\ &\\ &\text {Y por el teorema de los cosenos}\\ &\\ &d^2 = b^2+b^2 -2·b·b·\cos(180º-2x)=\\ &2b^2[1-\cos(180º-2x)]=\\ &2b^2(1-cos180º\cos 2x-sen180ºsen\,2x)=\\ &2b^2(1+\cos 2x)= 2b^2(2cos^2x)=\\ &4b^2cos^2x\\ &\\ &d = 2bcosx\\ &Como \;b= \frac{c}{seny}\\ &\\ &d= \frac{2·c·cosx}{seny}\\ &\\ &\text{Igualando las expresiones de d tenemos}\\ &\\ &\frac{c·seny}{cosx}=\frac{2·c·cosx}{seny}\\ &\\ &sen^2y=2cos^2x\\ &\\ &\cos^2x = \frac{sen^2y}{2}\\ &\\ &cosx= \frac{seny}{\sqrt 2}\\ &\\ &\text {llevamos este valor a la primera expresión de d}\\ &\\ &d= \frac{cseny}{\frac{seny}{\sqrt 2}}=c\sqrt 2\\ &\\ &Luego\\ &\\ &\frac dc = sqrtr 2\end{align}$$Y eso es todo. Espero que te sirva y lo hayas entendido. He usado diversas fórmulas trigonométricas y no puse muchos comentarios porque el editor de ecuaciones se bloquea si lo cargas mucho. Si no entendiste algo dímelo.
