Volumen de un solido por secciones.
Hallar el volumen de un solido que tiene por base la región del plano encerrada po 4y=x¨2 y la recta que pasa por (4,4)y (-2,1).sabiendo que toda región plana perpendicular al eje y es un triangulo isósceles con uno de sus catetos sobre el plano de la base. Mi duda es la siguiente, como calculo la h del triangulo para calcular el área?la base seria x=2y?esta bien si integro de 0a 1(de la función parabólica) y de 1a 4(de la recta)?
1 respuesta
Es un poco enrevesado el ejercicio.
Dice que las regiones perpendiculares al eje Y son "triángulos isósceles con uno de sus catetos sobre el plano de la base"
El único triángulo que es isósceles y rectángulo a la vez es el que tiene los dos catetos iguales, luego la base y la altura miden lo mismo con lo que el área de triangulo es (b^2)/2.
He hecho la gráfica y creo que tu también la has hecho por lo que dices.
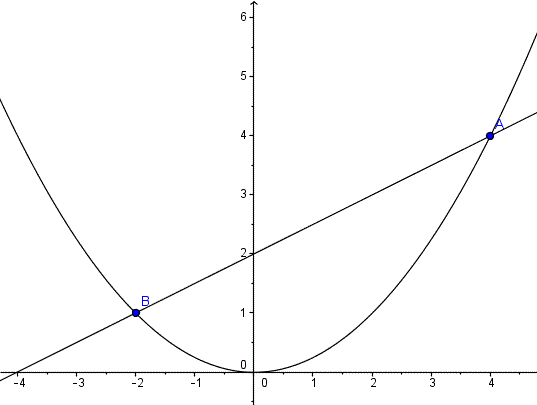
Hay que integrar a lo largo del eje Y. Y hay que hacer dos integrales ya que de 0 a1 los extremos de la base son los de la función parabólica y de 1 a 4 son la recta por la izquierda y la función parabólica por la derecha.
Para calcular esos extremos debes usar la función inversa
x = +- sqrt(4y) = +- 2sqrt(y)
Con lo que entre 0 y 1 la base mide 4sqrt(y) y el área es
16y/2 = 8y
Y la recta entre (-2,1) y (4,4)
y = 1 + [(4-1)/(4+2)](x+2) = 1+ x/2 +1 = 2 + x/2
y = x/2 + 2
Puesta en función de x es
x = 2y - 4
Y la distancia entre extremos será
2sqrt(y) - 2y + 4
el areá será
(2sqrt(y) - 2y + 4)^2 / 2 = (4y +4y^2 + 16 - 4ysqrt(y) +16sqrt(y) -16y)/2 =
2y^2 - 6y + 8 - 2y·sqrt(y) + 8sqrt(y)
Luego, si he hecho bien las cuentas, que tienes que revisarlas, el volumen será
$$\int_0^18y\,dy +\int_1^4 (2y^2 - 6y + 8 - 2y \sqrt y + 8 \sqrt y)dy$$
No es que sean muy difíciles pero lo suficiente para que te puedas liar al calcularlas. Si no te salen dímelo, y las calcularé con ordenador o a mano según sea la duda que tengas, que por menos de nada me lio con las cuentas y no me salen.
el área de un triangulo no es base x altura/2? o igual se puede expresar como lo expreso en el ejercicio?
Si, esa es la fórmula del área y eso hemos calculado, ten en cuenta que este triangulo tenía la misma base que altura. Como la base era 2sqrt(y)-2y+4 he puesto
Área = (2sqrt(y) - 2y + 4)^2 / 2 =
(4y +4y^2 + 16 - 4ysqrt(y) +16sqrt(y) -16y)/2 =
2y^2 - 6y + 8 - 2y·sqrt(y) + 8sqrt(y)
AH genial ahora si,. te hago una ultima pregunta si yo tengo que calcular el volumen de un solido (revolución) y la función es y = x^3/2 , x=-2 y el eje x . El primer volumen seria integrar de -2 a 0 y el segundo integrar de 0 a oo?
El dividir el intervalo de integración en dos o más se hace si la función cambia de signo. Entiendo que quieres decir en el intervalo [-2, +oo] y la función (x^3)/2, se debe hacer eso que dices porque antes del 0 es negativa y después positiva.
