Ayuda con geometría ?

Vamos a construirlo en el siguiente orden.

El origen será el punto B, el eje Y contendrá AB y el eje X contendrá BC

Tomaremos el punto M(m, m2) a distancia 4 del origen, por lo que todo dependerá de m

$$\begin{align}&M=\left(m,\sqrt{16-m^2}\right)\\ &\end{align}$$

Ahora calcularemos el punto A(0,a) situado a distancia 5 de M

$$\begin{align}&\sqrt{m^2+\left(a-\sqrt{16-m^2}\right)^2}=5\\ &\\ &\\ &m^2+\left(a-\sqrt{16-m^2}\right)^2 = 25\\ &\\ &\\ &m+a+16-m^2-2a \sqrt{16-m^2}=25\\ &\\ &\\ &a^2-2a \sqrt{16-m^2}-9 = 0\\ &\\ &\\ &a=\frac{2 \sqrt{16-m^2} \pm \sqrt{4(16-m^2)+36}}{2}\\ &\\ &\\ &a=\sqrt{16-m^2} \pm \sqrt{(16-m^2)+9}\\ &\\ &\\ &a=\sqrt{16-m^2} + \sqrt{25-m^2}\end{align}$$

Tomamos esa solución porque la otra era negativa y el punto A tiene coordenada positiva en y

Automáticamente hemos calculado ya el punto C

C=(a,0)

Y el punto N no es más que el escalar 2 multiplicando al vector BM

$$N=\left(2m,2 \sqrt{16-m^2}\right)$$

Lo que debe cumplirse para que todo encaje es que el punto N así calculado este a distancia "a" del punto C(a,0). Para no andar con raíces cuadradas impertinentes ya elevo al cuadrado en ambos lados

$$\begin{align}&(2m-\sqrt{16-m^2}-\sqrt{25-m^2})^2+(2 \sqrt{16-m^2}-0)^2=(\sqrt{16-m^2}+\sqrt{25-m^2})^2\\ &\\ &\text{Ya sabemos que el término derecho se simplificará con algo que saldrá} \\ &\text{en el izquierdo y no hay necesidad de operar ese cuadrado}\\ &\\ &\\ &4m^2 -4m(\sqrt{16-m^2}+\sqrt{25-m^2})+64-4m^2=0\\ &\\ &\\ &64 =4m(\sqrt{16-m^2}+\sqrt{25-m^2})\\ &\\ &\\ &16 =m(\sqrt{16-m^2}+\sqrt{25-m^2})\\ &\\ &\\ &256= m^2(16-m^2+25-m^2)+2m^2 \sqrt{(16-m^2)(25-m^2)}\\ &\\ &\\ &2m^4-41m^2+256 =2m^2 \sqrt{m^4-41m^2+400}\\ &\end{align}$$

$$\begin{align}&4m^8+1681m^4+ 65536-164m^6+1024m^4-20992m^2=4m^8-164m^6+1600m^4\\ &\\ &\\ &1105m^4-20992m^2 +65536=0\\ &\\ &m^2 =\frac{20992 \pm \sqrt{20992^2-4·1105·65536}}{2210}\\ &\\ &\\ &m^2 =\frac{20992 \pm 12288}{2210}=\frac{256}{17}\;\;y \;\;\frac{256}{65}\\ &\\ &\\ &m= \frac{16}{\sqrt{17}}\;\;y \;\;\frac{16}{\sqrt{65}}\\ &\\ &\\ &m= \frac{16 \sqrt{17}}{17}\;\;y\;\;\frac{16 \sqrt{65}}{65} \\ &\\ &\\ &m\approx 3.880570001\;\; y\;\;1.984555753\\ &\\ &\\ &\end{align}$$

¡Y aun queda calcular distancia(A,N), vaya problema!

Llegado aquí voy a hacer ya la gráfica, no sé si los puntos están bien calculados y antes de hacer más cuentas me aseguraré.

En Geogebra había hecho la gráfica tomando un valor m al azar en color naranja. Lo llamé M2 y todo lo naranja es el desarrollo. AL final N2 no está en la circunferencia que debería y por eso no sirve.

Pero los puntos que he calculado en rosa y azul sí cumplen que N y N1 están en sus respectivas circunferencias de puntos equidistantes que deben estar.

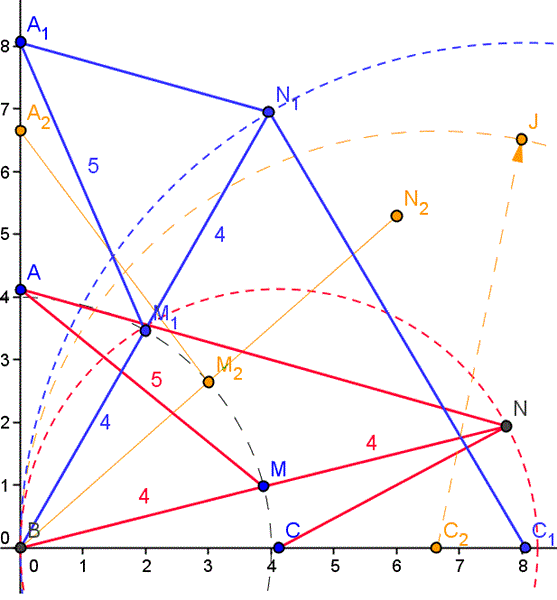
Vamos con las distancias que nos piden:

$$\begin{align}&A=\left( 0,\;\sqrt{16-\frac{16^2·17}{17^2}}+\sqrt{25-\frac{16^2·17}{17^2}} \right)= (0,\sqrt{17})\\ &\\ &\\ &N= \left( \frac{2· 16 \sqrt{17}}{17},\;\;2 \sqrt{16-\frac{16^2·17}{17^2} } \right)=\\ &\\ &\\ &\left( \frac{32· \sqrt{17}}{17},\;\;\frac{8 \sqrt{17}}{17} \right)\\ &\\ &\\ &\overline{AN}=\sqrt{\left(\frac{32 \sqrt{17}}{17}\right)^2+\left(\frac{8 \sqrt{17}}{17}-\sqrt{17}\right)^2}=\sqrt{65}\\ &\\ &\\ &\overline{AN} \approx 8.062257748\\ &\\ &\\ &\\ &\text {Esto es durísimo, si quires calcula } \overline{A_1N_1} \text{ como ejercicio}\\ &\text{El resultado es:}\\ &\\ &\overline{A_1N_1}=\sqrt{17} \approx 4.123105626\end{align}$$

Y eso es todo, espero que te sirva y lo hayas entendido. Muchos pasos se dieron aprisa porque es prácticamente imposible escribir, el ordenador va de pena con esta carga. Y también sirve para que hagas cuentas mentales o en papel, que no seas mero espectador.

Hay alguna expresión matemática muy larga que no cabra en una línea y aparecerá cortada, para verla tendrás que usar las barras de desplazamiento horizontal que hay al final de cada bloque, hice dos bloques en la parte larga en previsión de eso y ha salido bien ahora que se puede ver, que mientras lo escribes no sabes cómo quedará, solo una vez mandado se puede saber cómo quedaron las fórmulas.

wa!! pensé que iva ser mas fácil ,solo quería comprobar la respuesta porque estaba en duda y esta bien

yo lo hice de una manera un poco distinta

la imagen :

http://www.subeimagenes.com/img/img033-302658.html

traze del vértice A una perpendicular AP y del vértice C otra perpendicular CM (es isósceles el triangulo BNC)

luego aplico semejanza o congruencia(la verdad no se cual termino se usa ) a los triángulos BAP y BMC

luego uso los datos del problema y me sale sqrt[17] .

igual gracias ...

Los problemas de geometría pueden tener una complicación grandísima, sobre todo fuera de contexto, sin saber que teoremas y tipo de geometría se está utilizando en el capítulo del libro o apuntes. Se debería adjuntar qué métodos se están usando en problemas de este tipo.

Dices que BAP es semejante a BMC, más bien habría que escribir que BAP es semejante a CBM, hay que usar el mismo orden en los ángulos iguales de uno y otro triángulo.

Pero es que por más que lo intento, no veo que los dos ángulos que has marcado como alfa sean iguales de una forma inmediata o casi inmediata. ¿Podrías decirme porque son iguales?