Volumen de solido

La función es muy fácil pero hagamos la gráfica

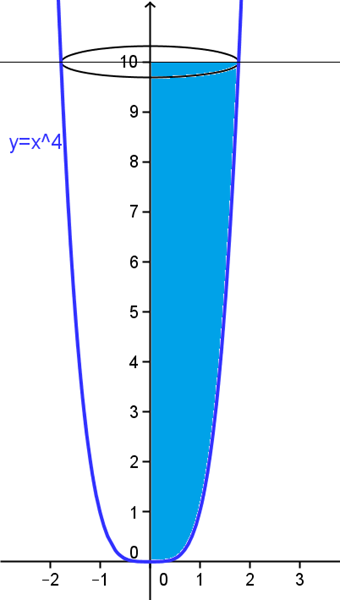
Cuando la función f(x) gira alrededor del eje X la integral es la de f(x) cuando la función g(x) gira alrededor del eje y la integral es con g(y)

Por tanto pondremos la función de "y" y los límites de integración en "y". Si nos han dado y=f(x) tenemos que la función respecto de y es g(y) = f^-1(y)

$$V=\pi\int_a^b [g(y)]^2dy$$

y= x^4 ==> x = y^(1/4)

g(y) = y^(1/4)

[g(y)]^2 = y^(1/2)

y los límites de integración son y=0, y=10

$$\begin{align}&V=\pi \int_0^{10}y^{\frac 12}dy =\pi \left[\frac 23y^{3/2}  \right]_0^{10}=\\ &\\ &\\ &\\ &\frac 23\pi \sqrt{1000}=\frac{20\pi \sqrt{10}}{3}\end{align}$$

Y eso es todo.