Derivadas - Puntos Máximos y Mínimos
teniendo en cuenta la función y= x^4/4 + x^3/3 - x^2
dados los intervalos
1. (0.54 , -0.166)
2. (1.2 , -0.633)
3.(- 2 , -2.666)
4.(1 , 1.083)
Donde ocurre un mínimo es en:
Respuesta 1y2 = A
Respuesta 2y3 = B
Respuesta 3y4 = C
Respuesta 2y4 = D
Madre mía, otro ejercicio con la misma función, ya estoy temblando.
Los máximos y mínimos relativos tienen la derivada nula
f '(x) = x^3 + x^2 - 2x = 0
Primeramente tenemos la solución x=0
dividimos entre x y queda
x^2+x-2 = 0
$$\begin{align}&x=\frac{-1\pm \sqrt{1+8}}{2}= -2\quad y\quad 1\\ &\end{align}$$y la derivada segunda es
f ''(x)=3x^2+2x-2
Calculamos el valor de la derivada segunda en esos puntos para saber si es máximo o mínimo
f ''(-2) =3(-2)^2+2(-2)-2 = 12-4-2 = 6 como es >0 es mínimo
f ''(0) = -2 como es menor que 0 es máximo
f ''(1) = 3+2-2 = 3 como es mayor que cero es mínimo
Luego los mínimos están en x=-2 y x=1
Calculamos esos puntos
f(-2) = (-2)^4/4 + (-2)^3/3 - 2^2 = 4 - 8/3 -4 = -8/3
f(1) = 1/4 + 1/3 - 1 = (3+4-12)/12 = -5/12
Los mínimos son
(-2, -8/3) y (1, -5/12)
que puestos con decimales son
(-2, -2.6666) y (1, -0.416666)
El primer punto aparece en las respuestas, pero el segundo no, Luego otra vez se han equivocado, vaya figura está hecho el responsable de ese enunciado y soluciones.
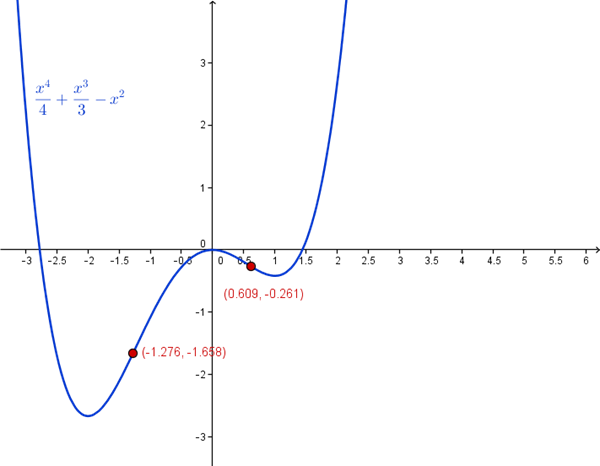
Te mando la misma gráfica que antes, que aunque los marcados son los puntos de inflexión, también sirve para ver cuál es el valor correcto del mínimo que hay en x=1.
Y eso es todo.
