Necesito por favor que me asesores en esta pregunta de cálculo, te daré máxima puntuación.

1) Los puntos críticos son aquellos que no tienen derivada o que la tienen y su valor es cero.

La función es perfectamente continua y derivable, luego los únicos puntos críticos son los que su derivada es cero.

f '(x) = 4x^3 -4x = 0

primero tenemos el punto critico x=0

Simplificamos x para calcular los otros dos

4x^2 -4 = 0

4x^2 = 4

x^2=1

x=1 y -1

Luego los puntos críticos son -1, 0 y 1.

2. LOs intervalos de crecimiento son aquellos donde la derivada es positiva y los de decrecimiento don es negativa. Ya tenemos los puntos donde la derivada vale cero, simplemente tomemos un punto dentro de cada intervalo para saber si la derivada es positiva o negativa

(-oo, -1) en -2 es 4(-2)^3 -4(-2) = -32+8 = -24 negativo luego decreciente

(-1, 0) en -1/2 es 4(-1/2)^3 -4(-1/2) = -1/2 + 2 = 3/2 positivo luego creciente

(0,1) en 1/2 es 4(1/2)^3 -4(1/2) 1/2 -2 = -3/2 negativo luego decreciente

(1,+oo) en 2 es 4·2^3 - 4·2 = 32-8= 24 positivo luego creciente

Luego los intervalos de crecimiento son (-1,0) y (1, +oo)

Y los de decrecimiento son (-oo, -1) y (0,1)

3)

Calculamos la derivada segunda y estudiaremos los puntos donde se anula. Si un punto se anula en la derivada segunda y luego la primera derivada que deja de ser nula es una derivada de orden impar impar es un puntos de inflexión

f ''(x) = 12x^2 -4

12x^2 - 4 = 0

12x^2 = 4

x^2 = 1/3

x= +- sqrt(1/3)

4) La concavidad y convexidad depende del signo de la derivada segunda. Pero como como libro y en especial los hispanos respecto de los anglosajones llaman convexidad a una cosa distinta, voy a decir que tiene forma de U cuando la derivada segunda es positiva y forma de signo de intersección cuando es negativa. Tu verás como te la definen a ti y usas la palabra adecuada

Tomamos los intervalos en que se divide la recta real por las raíces de la derivada segunda calculada en el apartado anterior

En (-oo,-sqrt(1/3)) en -1 es 12-4 = 8 positiva, forma de U

En (-sqrt(1/3), sqrt(1/3)) en 0 vale -4 negativa, forma de intersección

En (sqrt(1/3), +oo) en 1 vale 12-4=8 positiva, forma de U

Luego tiene forma de U en (-oo,-sqrt(1/3)) y (sqrt(1/3), +oo)

Y forma de signo de intersección en (-sqrt(1/3), sqrt(1/3))

5. Para el bosquejo tendríamos en cuenta todo lo que hemos calculado. Añadiríamos los valores de la función en los puntos críticos para obtener los puntos

(-1,-1)

(0,0)

(1,-1)

Y tener en cuenta que sqrt(1/3) = 0.57735

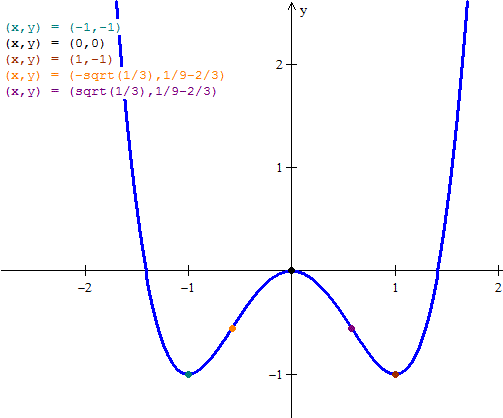
Y eso es todo.