Dudas sobre respuesta ya calificada de calculo
Tengo dudas, al verificar me percate de que tomaste el punto (1,1) pero en el enunciado es (-1,1) me podrías confirmar por favor?
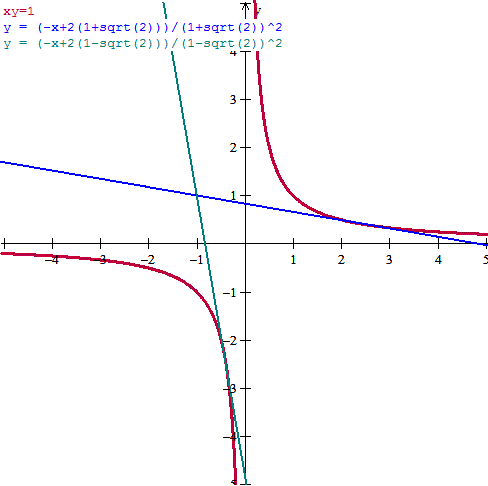
Hallar las ecuaciones de las rectas tangentes de la función implícita xy=1 y que pasan por el punto (-1,1)
1 respuesta
Respuesta de Valero Angel Serrano Mercadal
1