Gráficas de Parábolas

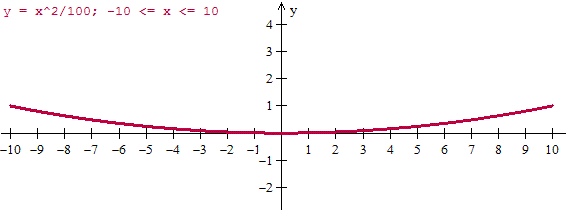
Pues lo principal es saber que es una parábola. Que tiene un eje paralelo al eje Y como longitudinal. Si el longitudinal fuera el X la ecuación sería así X= (1/100)x^2.

Y como el coeficiente es positivo tiene forma de U, si fuese negativo la forma sería una U hacia abajo.

Y luego se ve fácilmente que pasa por (0,0). Además como el valor de Y es siempre positivo el punto (0,0) es el mínimo y es el vértice de la parábola y con ello ya se sabe que el eje longitudinal es el propio eje Y.

Eso de que el eje longitudinal es Y se podría haber sabido también porque ña función tiene simetría respecto de y ya que f(x) = f(-x)

Y luego ya pongamos los puntos que necesitemos para hacer bien la gráfica. Por ejemplo los extremos son (-10, 1) y (10, 1), puntos intermedios serían (-5, 0.25) y (5, 0.25) y si necesitas más calculas más

Ahora que hablas de Antena, quizá necesites conocer el foco de la parábola ya que es donde rebotan todas las ondas que recoge la antena.

La ecuación canónica de una parábola de este tipo es

x^2 = 2py

Donde la distancia del foco al centro es p/2

Luego está parábola tiene ecuación canónica

x^2=100y = 2·50y

luego p=50

luego p/2 = 25

Y el foco estará en el punto (0, 25)

Y la directriz será la recta y=-25

Y eso es todo, espero que te sirva y lo hayas entendido. SI necesitas algo mas en este ejercicio dímelo.