Calcular el área de un recinto limitado

Puede intuirse mentalmente sin hacer la gráfica, pero mejor hacerla para verlo claramente.

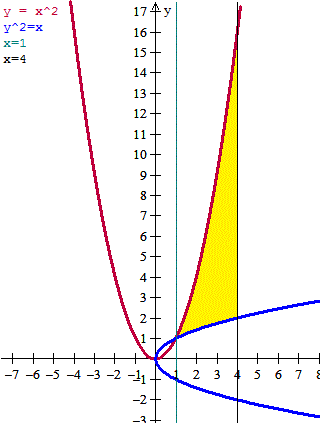
La curva y^2 =x debe expresarse como función de x

y = sqrt(x)

También podría haber sido y=-sqrt(x) pero por la gráfica se ve que la rama de la curva y^2=x que limita el área es la de signo positivo

Y como las funciones no se cortan dentro del intervalo de integración el área es la integral definida de la función superior menos la inferior. O también se puede usar el valor absoluto de la integral y así no no s preocupamos del orden de la resta.

$$\begin{align}&Área=\int_1^4 (x^2-\sqrt x)dx=\\ &\\ &\\ &\int_1^4(x^2-x^{\frac 12})dx=\\ &\\ &\\ &\left[\frac {x^3}{3}-\frac{x^{\frac 32}}{\frac 32}  \right]_1^4=\left[\frac {x^3}{3}-\frac{2x^{\frac 32}}{3}  \right]_1^4=\\ &\\ &\\ &\frac{64}{3}-\frac{2·\sqrt{4^3}}{3}-\frac 13+\frac 23=\\ &\\ &\\ &\frac{64}{3}-\frac{16}{3}-\frac 13+\frac 23=\frac {49}{3}\\ &\\ &\end{align}$$

Y eso es todo.