Siendo f(0)=pi y f´(equis)=1/equis al cuadrado +1,graficar la F f(equis); f´(equis)

Creo que ha quedado claro. Una observación únicamente, todo numerador que se componga de mas de un termino y todo denominador que se componga de más de un término o factor debe encerrarse entre paréntesis. Ya que si no las normas imperantes (que se usan tanto por las personas que las conocen como por los ordenadores y calculadoras) hacen que los numeradores tomen solo el último término antes de la / y los denominadores el primer término tras ella y si es denominador es un producto se toma solo el primer factor

Ejemplos:

A la derecha está la interpretación que se da

1 / x^2 + 1 = (1/x^2) + 1

1 / 2x = (1/2)x

1+x / 1-x = 1 + (x/1) - 1 = x

Como yo creo que tú has querido que el denominador sea x^2 +1 deberías haber escrito

f '(x) = 1 / (x^2+1)

Vayamos ya al ejercicio:

Para calcular f hay que hacer la integral indefinida. Como la integral indefinida nos da la función mas una constante cualquiera nos serviremos del valor que nos dan para f(0) para calcular la constante. La integral es fácil, es inmediata.

$$\begin{align}&f(x)=\int \frac{dx}{x^2+1}=arctg\,x+C\\ &\\ &\\ &Como\; f(0)=\pi \;tenemos\\ &\\ &f(0)=arctg\, 0 + C = \pi\\ &\\ &Como\; arctg\,0 = 0\\ &\\ &f(0) = 0+C=\pi\\ &\\ &c=\pi\\ &\\ &\text{y sustutiyendo la constante en la función tenemos}\\ &\\ &f(x) = arctg(x)+\pi\end{align}$$

Y estas son las gráficas

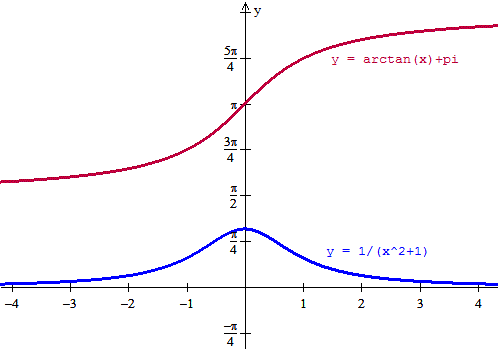
Y eso es todo.

hola, muchas gracias, entendí todo pero me quedo solo una duda con los gráficos, los hiciste aproximados, dándole valores a "X" o de otra forma?

Los hice con un programa de gráficas llamado Winplot.

Consideré que lo importante del problema era hallar la función f. Y como no decías nada de cómo graficar pensé que se podía hacer de cualquier forma.

Si quieres que lo haga con estudio del dominio, imagen, continuidad, cortes con los ejes, asíntotas, máximos, mínimos, crecimiento, decrecimiento, concavidad, convexidad y encima para dos funciones tendrías que mandar dos preguntas más, lleva bastante trabajo hacer eso aunque sea sencillo.