Determinación de distribuciones limites
la pregunta es
http://www.guardarimagenes.com.ar/image/fotos/71173e60ff9389693816.png
1 respuesta
Hagamos la gráfica.
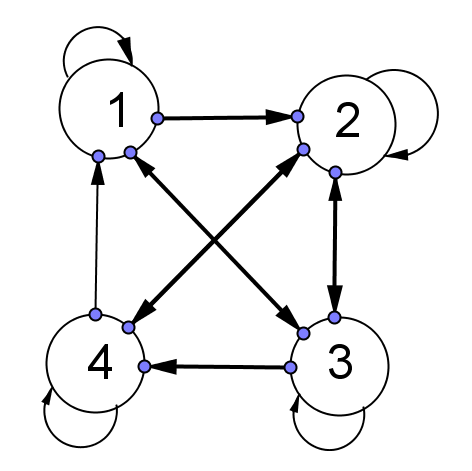
Todos están comunicados. En la matriz solo faltaban:
1-->4 que se obtiene por el camino 1-->3-->4
2 -->1 que se obtiene por 2-->4-->1
4 -->3 que se obtiene por 4-->2-->3
Luego hay una única clase de comunicación {1,2,3,4}
Luego es una cadena irreducible. Y es recurrente y por ser un número de estados finito es recurrente positiva.
Y es aperiódica porque al 1 puede volver mediante 1-->3-->1 y mediante 1-->3-->4-->1, eso es en 2 o en 3 pasos y el mcd(2,3)=1
Por la proposición 6 una cadena de Markov irreducible y recurrente positiva tiene una unica distribución invariante cuyo elemento j-esimo es el inverso del tiempo esperado del estado j.
Calculemos la distribución invariante
V·P = V
Esto ya lo hemos hecho alguna vez. Las ecuaciones que quedan son los coeficientes de las columnas puestos por filas y restando 1 en los coeficientes de la diagonal principal
-3/4 0 1/4 1/4 | 0
1/4 -3/4 1/4 1/4 | 0
1/2 1/2 -3/4 0 | 0
0 1/4 1/4 -1/2 | 0
-3 0 1 1 | 0
1 -3 1 1 | 0
2 2 -3 0 | 0
0 1 1 -2 | 0
0 -9 4 4 | 0
1 -3 1 1 | 0
0 8 -5 -2 | 0
0 1 1 -2 | 0
0 0 13 -14 | 0
1 -3 1 1 | 0
0 0 -13 14 | 0
0 1 1 -2 | 0
Tomamos v4 como parámetro
13v3 = 14v4
v3 = (14/13)v4
v2 = -v3+2v4 = (-14/13 +2)V4 = (12/13)v4
v1 = 3v2 - v3 -v4 = (36/13 -14/13 - 1)v4 = (9/13)v4
La suma de los 4 debe ser 1
(9/13 + 12/13 + 14/13 + 1)v4= 1
(48/13)v4=1
v4 = 13/48
v3 = 14/48
v2 = 12/48
v1 = 9/48
Como esto son los inversos del tiempo esperado, tendremos
1/mu1 = 9/48 ==>
mu1 = 48/9 = 16/3
mu2 = 48/12 = 4
mu3 = 48/14 = 24 / 7
mu4 = 48/13
Y para calcular la proporción calculamos la suma de los 4 mus
16/3 + 4 + 24/7 + 18/13 = 3862/273
y cada mu se divide entre la suma de ellos
p1 = (16/3) / (3862/273) = 728/1931
p2 = 4 / (3862/273) = 546/1931
p3 = (24/7) / (3862/273) = 468/1931
p4 = (48/13) / (3862/273) = 504/931
A la larga la matriz de transición elevada a la n tiende a tener todas las filas iguales a la distribución invariante, luego será
9/48 12/48 14/48 13/48
9/48 12/48 14/48 13/48
9/48 12/48 14/48 13/48
9/48 12/48 14/48 13/48
Las mejoras son los pasos de 3 ó 4 a 1 ó 2
3a1 = 9/48
3a2 = 12/48
4a1 = 9/48
4a2 = 12/48
Su suma es 42/48 = 7/8
Como son 4 filas que cada una suma 1 la suma de las probabilidades de todos los cambios de estado posibles es 4, luego la proporción de las mejoras es
(7/8) / 4 = 7/32
A la larga ee mejorará 7 de cada 32 veces.
Y eso es todo, si hay alguna forma más rápida de hacerlo no lo sé, solo sé que hasta anteayer no sabía nada de esto.
