Sólidos de revolución.
Que tal valeroasm, mi pregunta es la siguiente:
Calcúlese el volumen del solido generado al girar alrededor del eje x de la
región acotada por la parábola y=x²+1 y la recta y=x+3
de antemano te agradezco tu ayuda, gracias te mando un saludo.
Respuesta de Valero Angel Serrano Mercadal
1
Hacemos la gráfica para entenderlo mejor.
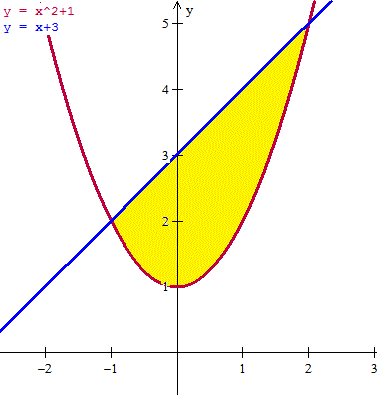
En amarillo eta el área que engendrar el volumen al girar. Vamos a calcular los punto de intersección aunque se vean
x^2 + 1 = x+3
x^2 - x - 2 = 0
x=[1 +- sqrt(1+8)]/ 2 = (1 +-3)/2 = 2 y -1
El volumen será el volumen generado por la recta entre -1 y 2 menos el generado por la parábola entre -1 y 2
La fórmula de volumen generado por una función es:
$$\begin{align}&V=\pi\int_a^b[f(x)]^2dx\\ &\\ &\\ &V=\pi\int_{-1}^2(x+3)^2dx-\pi\int_{-1}^2(x^2+1)^2dx =\\ &\\ &\pi\int_{-1}^2(x^2+6x+9 -x^4-2x^2-1)dx =\\ &\\ &\pi\int_{-1}^2(-x^4-x^2+6x+8)dx=\\ &\\ &\pi\left[-\frac{x^5}{5}-\frac{x^3}{3}+3x^2+8x \right]_{-1}^2=\\ &\\ &\pi \left(-\frac{32}{5}-\frac 83+12+16-\frac 15-\frac 13-3+8 \right)=\\ &\\ &\pi \left(-\frac{33}{5}-\frac 93+33 \right)=\\ &\\ &\pi \left(-\frac{33}{5}+30 \right)=\\ &\\ &\frac{117}{5}\pi\end{align}$$Y eso es todo.
