Necesito resolver este ejercicio
encuentre los ángulos interiores de los triángulos cuyos vértices son : a) (4,2) (0,1) (6,-1)
b) (-3,-1) (4,4) (-2,3) x fa muchas gracias x la ayuda
Haremos uno porque los dos son iguales. Si quieres que haga el otro mándalo en otra pregunta distinta.
Ponemos nombre a los puntos
A=(4, 2), B=(0,1), C=(6,-1)
Para el ángulo en el vértice A necesitamos las pendientes de AB y AC
p(AB) = (1-2)/(0-4) = 1/4
p(AC) = (-1-2)/(6-4) = -3/2
Estas pendientes son las tangentes de dos rectas, la tangente del angulo entre ellas se puede calcular con la fórmula
$$\begin{align}&tg(a-b)=\frac{tga-tgb}{1+tga·tgb}= \\ &\\ &\frac{\frac 14+\frac 32}{1-\frac 14 ·\frac 32}= \frac{\frac 74}{\frac 58}= \frac{7·8}{4·5}= \frac{56}{20}=\frac{14}{5}\\ &\\ &\text{Y calculamos el arcotangente o inversa de la tangente}\\ &\\ &arctg(14/5) = 70,346176º\end{align}$$En estos problemas es imprescindible hacer el dibujo del triángulo porque la fórmula nos da siempre el ángulo menor y debemos comprobar si ese es el angulo interno o es el exterior.
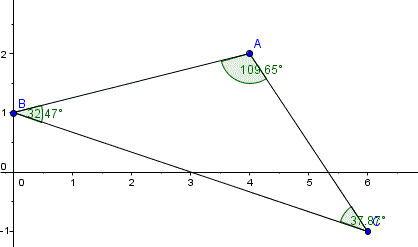
En este caso se mira y se ve que el interno tiene más de 90º, luego la fórmula nos ha dado el exterior. El interno se calcula como 180º-exterior
Angulo interno en A = 180º - 70,346176 = 109,65382º
Para el ángulo en B necesitamos las pendientes de AB y BC
La de AB ya estaba calculada 1/4
La de BC es [-1-1] / 6 = -1/3
Y hacemos la misma cuenta que con el otro ángulo:
$$\begin{align}&tg(a-b)=\frac{tga-tgb}{1+tga·tgb}= \\ &\\ &\frac{\frac 14+\frac 13}{1+\frac 14·\frac 13}=\frac{\frac {7}{12}}{\frac{11}{12}}= \frac{7}{11}\\ &\\ &\\ &arctg(7/11) = 32,471192º\end{align}$$Aquí no hace falta mirar, con todo lo que mide el ángulo A es imprescindible que los otros dos midan menos de 90º, luego el que ha salido es el interno
Luego los ángulos son:
A = 109,65382º
B = 32,471192º
C = 180º-A-B = 37.874984
Y eso es todo.
