Calculo diferencial e Integral: Límites.
Hola experto, espero puedas ayudarme con estos límites de funciones. Agradeceré mucho una pronta respuesta de tu parte, ya que comienzo a estudiar nuevamente despue´s de mucho tiempo.
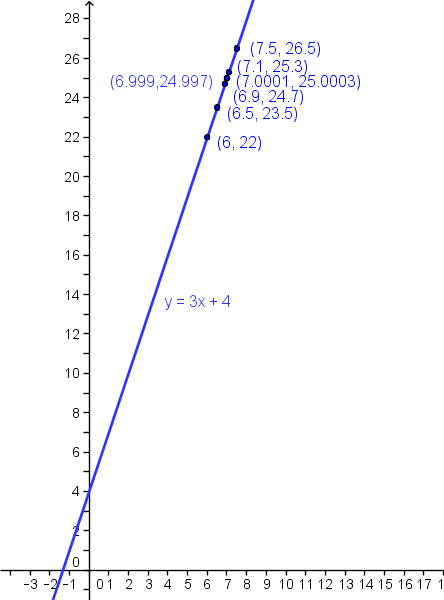
en la función f(x)=3x+4, a qué valor tiende “y” cuando “x” tiende a 7
x f(x) f(x)=3x+4
6
6.5
6.9
6.999
7.0001
7.1
7.5
Completa la tabla, gráfica la función y encuentra el límite de las siguientes funciones:
a)
$$f(x)=x2-4 si "x" tiende a 1$$
b)
$$f(x)= 2x3, si "X" tiende a "-2"$$
c)
$$f(x)= 1/(x-1) si X tiende a 1$$
Saludos experto! Gracias de antemano.
1 respuesta
La función f(x) = 3x+4 es una recta, es una función continua donde las haya y los límites coinciden con el valor de la función en el punto.
$$\lim_{x\to 7}\;(3x+4) = 3·7+4 = 25$$La tabla se hace fácilmente
x | lim f(x) ------------------- 6 | 3·6+4 = 22 6.5 | 23.5 6.9 | 24.7 6.999 | 24.997 7.0001 | 25.0003 7.1 | 25.3 7.5 | 26.5
Y la gráfica es esta, hay dos puntos indistinguibles por estar muy juntos.
----------------------------
$$\lim_{x\to 1} (x^2-4) =1^2-4=-3$$$$\lim_{x \to -2} 2x^3=2(-2)^3 = 2(-8) = -16$$$$\lim_{x \to 1} \frac{1}{x-1}=\frac{1}{1-1}=\frac 10 = \infty$$Y eso es todo, espero que te sirva y lo hayas entendido. Si no, pregúntame. Y si ya está bien, no olvides puntuar.
Muchas gracias, con el primero que he visto tomé valor y decidí completar las otras.
Saludos cordiales experto! Nuevamente muchas gracias.
