Solución ejercicio 1c pagina 337

$$\begin{align}&\int_0^1\int_1^{e^x}(x+y)dydx=\\ &\\ &\int_0^1\left[xy+\frac{y^2}{2}\right]_1^{e^x}dx=\\ &\\ &\int_0^1\left(xe^x+\frac{e^{2x}}{2}-x-\frac 12\right)dx=\\ &\\ &\left[\frac{e^{2x}}{4}-\frac{x^2}{2}-\frac x2\right]_0^1+\int_0^1 xe^xdx=\\ &\\ &u=x\quad\quad\quad du=dx\\ &dv=e^xdx\quad v =e^x\\ &\\ &=\frac{e^2}{4}-\frac 12-\frac 12-\frac 14+\left[xe^x-e^x\right]_0^1=\\ &\\ &\frac{e^2}{4}-\frac 54+e-e-0+1=\frac{e^2-1}{4}\end{align}$$

Este es el dominio.

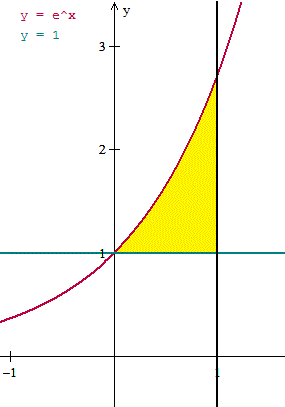
Es y-simple porque 1 <= e^x en el intervalo [0,1]

Es x-simple porque lnx <=1 en el intervalo [1,e]

Luego es una región simple.

Y eso es todo.