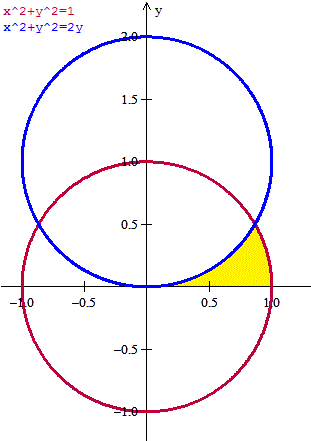Solución ejercicio 32 pagina 381

a) Esta es la región, la de color amarillo

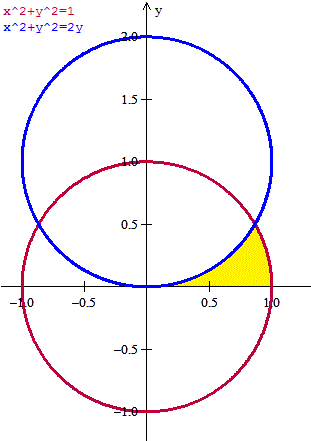
b)

u= x^2 + y^2

v = x^2 + y^2 - 2y

x vale entre 0 y 1

y valé entre 0 y dos funciones

Vamos a calcularlo bien

El punto de intersección es

1=2y

y=1/2

x = sqrt(1-1/4) = sqrt(3)/2

La parte inferior de la circunferencia azul es

$$\begin{align}&y^2-2y+x^2=0\\ &\\ &y=\frac{2-\sqrt{4-4x^2}}{2}=1-\sqrt{1-x^2}\end{align}$$

Entonces los límites superiores tras el cambio serán

$$\begin{align}&Si\;x \in\left[0,\frac{\sqrt 3}{2}\right]\implies y\in \left[0,1-\sqrt{1-x^2}\right]\\ &\\ &\\ &\\ &Si\;x \in\left[\frac{\sqrt 3}{2},1\right]\implies y\in \left[0,\sqrt{1-x^2}\right]\\ &\\ &-----------------\\ &\\ &Con\; x \in\left[\frac{\sqrt 3}{2},1\right]\\ &\\ &u=x^2+y^2=x^2+(1-\sqrt{1-x^2})^2=\\ &x^2+1-2 \sqrt{1-x^2}+1 -x^2= 2\left(1-\sqrt{1- x^2}\right)\\ &\\ &\\ &\\ &v=x^2+y^2-2y=2\left(1-\sqrt{1- x^2}\right)-2y=\\ &2\left(1-\sqrt{1- x^2}\right)-2\left(1-\sqrt{1- x^2}\right)=0\\ &\\ &\text{Es la función v=0}\\ &\\ &------------\\ &\\ &Con\; x \in \left[\frac{\sqrt 3}2,1\right]\\ &\\ &\\ &u=x^2+y^2 = x^2+1-x^2 =1\\ &v=x^2+y^2-2y=1-2y=1-2 \sqrt{1-x^2}\\ &\\ &\text{Es la recta u=1}\\ &\\ &\end{align}$$

Mientras que el eje X que era ek límite inferior se transforma en

u=x^2+y^2 = x^2+0 = x^2

v=x^2+y^2-2y = x^2+0-0 = x^2

Esto es la recta v=u

Con las rectas v=0, u=1 y v=u tenemos la región D que nos piden. Es un triángulo con vértices (0,0), (1,0) y (1,1) fácil de dibujar a mano.

c) El dominio de integración tras el cambio será

u € [0,1]

v € [0,u]

Calculamos el jacobiano del cambio

u = x^2 + y^2

v = x^2 + y^2 - 2y

u-v = 2y

y = (u-v)/2

x= sqrt(u-y^2) = sqrt[u - (u^2+v^2-2uv)/4]= (1/2)sqrt(4u-u^2-v^2+2uv)

Y calculamos las derivadas parciales del jacobiano

$$\begin{align}&\frac{\partial x}{\partial u}=\frac 12· \frac{4-2u+2v}{2 \sqrt{4u-u^2-v^2+2uv}}\\ &\\ &\\ &\frac{\partial x}{\partial v}=\frac 12·\frac{-2v+2u}{2 \sqrt{4u-u^2-v^2+2uv}}\\ &\\ &\\ &\\ &\frac{\partial y}{\partial u}= \frac 12\\ &\\ &\\ &\frac{\partial y}{\partial v}=-\frac 12\\ &\\ &\\ &J=\frac{\partial x}{\partial u}\frac{\partial y}{\partial v}-\frac{\partial x}{\partial v}\frac{\partial y}{\partial u}=\\ &\\ &\\ &-\frac 14·\frac{4-2u+2v-2v+2u}{2 \sqrt{4u-u^2-v^2+2uv}}=\\ &\\ &\\ &-\frac{1}{2 \sqrt{4u-u^2-v^2+2uv}}\end{align}$$

La integral será

$$\begin{align}&\int_0^1\int_0^u \frac 12 \sqrt{4u-u^2-v^2+2uv}\quad e^{(u-v)/2}\left(-\frac{1}{2 \sqrt{4u-u^2-v^2+2uv}}\right)dv\,du=\\ &\\ &-\frac 14\int_0^1\int_0^u e^{(u-v)/2}dv\,du=-\frac 14\int_0^1\left[-2e^{(u-v)/2}  \right]_0^u du=\\ &\\ &\frac 12\int_0^1 (1-e^{u/2})du=\frac 12\left[u-2e^{u/2}  \right]_0^1= \frac 12(1-2 \sqrt e-0+2e^0)=\\ &\\ &\\ &\frac 32-\sqrt e\\ &\\ &\\ &\end{align}$$

¡Uff! Revísalo porque no estoy seguro, pero estoy tan cansado que no puedo revisarlo.