Halla la ecuación de la elipse de vertices

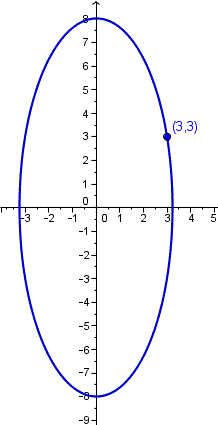
Los vértices están sobre el eje Y y son simétricos respecto de (0,0), luego es una elipse centrada mal alta que ancha. Su semieje mayor mide 8. Su ecuación canónica será

y^2 / 64 + x^2 / b^2 = 1

Y por pasar por punto (3,3) se cumple

9/64 + 9/b^2 = 1

9/b^2 = 1 - 9/64 = (64-9)/64 = 55/64

b^2 = 9/(55/64) = 9·64/55 = 576/55

Luego la ecuación es

y^2/64 + x^2 / (576/55) = 1

Puesta en forma general sería

y^2/64 + 55x^2/576 = 1

9y^2 + 55x^2 = 576

Para hacernos idea de la longitud sel semieje menor es:

sqrt(576/55) = sqrt(10.47272...) = 3.236159

Y la gráfica es esta

Y eso es todo.