Ecuación algebraica fraccionaria
Hola valeroasm, un gusto saludarlo. Me puede ayudar con esta ecuación por favor?
$$(w+1)/(w^2-w-2) -1/4=w^3-4w^2/2w^2-w^3$$
Saludos.
1 Respuesta
No tengo claro cuál es la expresión me parece que faltan paréntesis. Mira a ver si es esto.
$$\frac{w+1}{w^2-w-2}-\frac 14=\frac{w^3-4w^2}{2w^2-w^3}$$Te escribo la expresión en lenguaje del editor de ecuaciones para que aprendas como se ponen las fracciones de modo que salga la barra horizontal.
frac{w+1}{w^2-w-2}-frac 14=frac{w^3-4w^2}{2w^2-w^3}
Si, esa esa. Y gracias por lo del código.
Primero simplificaremos el termino derecho dividiendo numerador y denominador por w^2
$$\begin{align}&\frac{w+1}{w^2-w-2}-\frac 14=\frac{w-4}{2-w}\\ &\\ &\text{Ponemos denominador comun en el izquierdo}\\ &\\ &\\ &\frac{4(w+1)-w^2+w+2}{4(w^2-w-2)}=\frac{w-4}{2-w}\\ &\\ &\\ &\\ &\frac{4w+4-w^2+w+2}{4w^2-4w-8}=\frac{w-4}{2-w}\\ &\\ &\\ &\frac{-w^2+5w+6}{4w^2-4w-8}=\frac{w-4}{2-w}\\ &\\ &\\ &(-w^2+5w+6)(2-w) =(4w^2-4w-8)(w-4)\\ &\\ &-2w^2+10w+12+w^3-5w^2-6w =4w^3-4w^2-8w-16w^2+16w+32\\ &\\ &w^3-7w^2+4w+12=4w^3-20w^2+8w+32\\ &\\ &-3w^3 +13w^2-4w-20=0\\ &\\ &3w^3-13w^2+4w+20=0\\ &\\ &\end{align}$$Y la ecuaciones de grado 3 no son fáciles. O se resuelven con una fórmula muy compleja o con el ordenador. Solo en algún caso podremos dar con alguna respuesta entera, este es uno de ellos. He de confesarte que lo he resuelto con el ordenador por eso se cuáles son.
Habría que probar con los divisores de 20 que son 1,2,4,5,10,20 y los respectivos negativos y sucede que -1 la cumple
3 -13 4 20
-1 -3 16 -20
----------------
3 -16 20 0Y podríamos seguir por Ruffini, pero lo lógico es resolver la ecuación de segundo grado del polinomio que queda.
$$\begin{align}&3w^2-16w+20 = 0\\ &\\ &w=\frac{16\pm \sqrt{256-240}}{6}= \\ &\\ &\frac{16\pm4}{6} = \frac{20}{6}\;y\;2 = \frac{10}{3}\; y\; 2\end{align}$$Luego las tres respuestas momentáneamente son
x1 = -1
x2 = 10/3
x3 = 2
Pero hay que comprobar, porque en las ecuaciones con incógnitas en los denominadores o en las que tienen radicales u otras se pueden introducir soluciones fantasma, que verifican la ecuación a la que hemos llegado pero no verifican la ecuación inicial.
Y se comprueba que para x=-1 no se cumple porque tendremos
0/0 en el primer término
es una discontinuidad evitable, dividamos por x+1 numerador y denominador
1 -1 -2
-1 -1 2
---------
1 -2 0luego w^2 - w - 2 = (w+1)(w-2) y la simplificación queda
$$\begin{align}&\frac{1}{w-2}-\frac 14=\frac{w-4}{2-w}\\ &\\ &\text{Que evaluada en (-1) es}\\ &\\ &-\frac 13 - \frac 14 =-\frac{5}{3}\\ &\\ &-\frac{4+3}{12} = -\frac 53\\ &\\ &-\frac{7}{12}=-\frac 53\end{align}$$Lo cual es falso, luego (-1) no sirve de respuesta
En la misma expresión simplificada que acabamos de usar podemos evaluar el valor w=2
Y sucede que tendremos un
1/0 -1/4 = -2/0
Y aquí no hay simplificación que evite el cero del denominador, luego la función no esta definida en w=2 y no puede ser respuesta
Y solo nos queda la respuesta 20/6.
$$\begin{align}&\frac{1}{\frac{20}{6}-2}-\frac 14 = \frac{\frac{20}{6}-4}{2 -\frac{20}{6}}\\ &\\ &\frac{1}{\frac 86}-\frac 14 =\frac{-\frac 46}{-\frac 86}\\ &\\ &\frac 68 - \frac 14 = \frac 48\\ &\\ &\frac{6-2}{8}=\frac 48\\ &\\ &\frac 48 = \frac 48\end{align}$$Esta si que sirve.
Luego la única solución es w = 20/6
Puede comprobarse que es verdad haciendo la gráfica de la función.
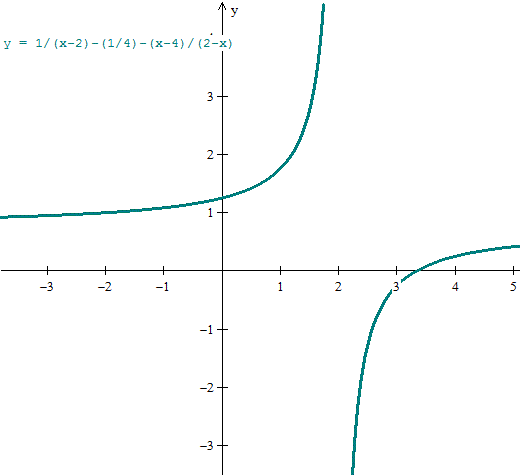
Y eso es todo.
