Calcula el volumen generado por las curvas dadas alrededor del eje x.

Son curvas girando alrededor del eje X, entonces debemos expresarlas como función de x para las integrales

y = 3- x

x=4-(y-1)^2

(y-1)^2=4-x

y-1=+-sqrt(4-x)

y = 1 +- sqrt{4-x}

Y estas funciones conviene dibujarlas si se quiere enterar uno.

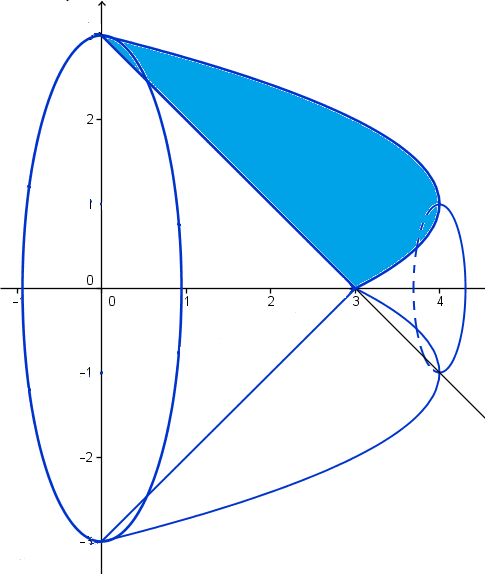
La pieza maciza completa sería generada por la función

y = 1 + sqrt{4-x} entre x=0 y x=4

El hueco de la izquierda es generado por la función

y= 3-x entre x=0 y x=3

El hueco de la derecha es generado por la función

y = 1 - sqrt(4-x) ente x=3 y x=4

Al volumen primero se le restan los de los huecos

$$\begin{align}&V_T=\pi\int_0^4(1+\sqrt{4-x})^2dx =\\ &\\ &\pi\int_0^4(1+4-x+2 \sqrt{4-x})dx=\\ &\\ &\pi\left[5x-\frac{x^2}{2}-2·\frac 23(4-x)^{3/2} \right]_0^4=\\ &\\ &\pi \left(20-8+\frac 43·8\right)=\\ &\\ &\pi\left(12+\frac{32}{3}  \right)=\frac{68\pi}{3}\end{align}$$

El del hueco izquierdo es

$$\begin{align}&V_{Izq}=\pi\int_0^3 (3-x)^2dx=\\ &\\ &\pi\left[-\frac{(3-x)^3}{3}  \right]_0^3= 9\pi\\ &\\ &\end{align}$$

Para el hueco derecho la función es muy parecida a la que integramos al principio salvo algún signo.

$$\begin{align}&V_{Der}=\pi\int_3^4(1-\sqrt{4-x})^2dx =\\ &\\ &\pi\int_3^4(1+4-x-2 \sqrt{4-x})dx=\\ &\\ &\pi\left[5x-\frac{x^2}{2}+2·\frac 23(4-x)^{3/2} \right]_3^4=\\ &\\ &\pi \left(20-8-15+\frac 92-\frac 43\right)=\\ &\\ &\pi\left(-3+\frac 92- \frac 43  \right)=\\ &\\ &\pi\left(\frac{-18+27-8}{6}  \right)=\frac{\pi}{6}\end{align}$$

Y ya solo queda restar los huecos a la pieza maciza

$$\begin{align}&V=\frac{68\pi}{3}-9\pi-\frac{\pi}{6}=\\ &\\ &\pi\left(\frac{136-54-1}{6}  \right)=\\ &\\ &\frac{81\pi}{6}=\frac{27\pi}{2}\end{align}$$

Y eso es todo, espero que te sirva y lo hayas entendido. Creo que es bastante más complicado que lo que hiciste.