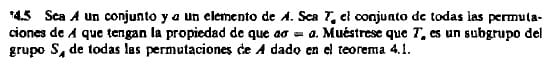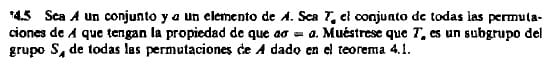El texto está muy borroso, no entiendo la propiedad de que dices. Por otro lado hablas de un teorema 4.1, pero yo no puedo saber qué teorema es ese.
Si sabes que el libro está en internet podrías darme el link, y si no escribe el problema a mano para poder entenderlo y cuéntame lo que haga falta del teorema 4.1 si es necesario.
No sé si será esto.
Para comprobar si un conjunto H es un subgrupo de G hay que demostrar dos cosas
i) Que H no está vacío
Ii) Que dados dos elementos b y c de H se cumple bc' € H.
Es un teorema de caracterización de subgrupos que seguramente habrás dado
La primera condición se cumple porque la permutación identidad pertenece a Ta.
Ahora la segunda.
Sean alfa y beta permutaciones de Ta
alfa(a) = a
beta(a) = a ==>
beta'(beta(a)) = beta'(a) ==>
(beta' · beta)(a) = beta'(a) ==>
Identidad(a) = beta'(a)
a = beta'(a)
Y entonces:
(alfa·beta')(a) = alfa(beta'(a)) = alfa(a) = a
Luego alfa·beta' € Ta
Y eso es todo, creo que eso pedían. Me parece que no he usado la notación del libro, por eso sería bueno si lo pudiera tener y porque yo no tengo libros de álgebra de mi época de estudiante y los apuntes están ilocalizables.