Cómo obtener la función inversa de y=por^2-4x+3;

La función inversa consiste en poner la y como función de x, es decir, despejar la x.

$$\begin{align}&y =x^2-4x+3\\ &\\ &x^2-4x +3-y=0\\ &\\ &x=\frac{4\pm \sqrt{16-12+4y}}{2}=\\ &\\ &\frac{4\pm \sqrt{4+4y}}{2}=\\ &\\ &\frac{4\pm2 \sqrt{1+y}}{2}=\\ &\\ &\frac{}{}2\pm \sqrt{1+y}\end{align}$$

Y para que la función inversa tenga la variable x se cambia la y por x y la x por f^-1(x)

$$f^{-1}(x)=2\pm \sqrt{1-x}$$

En realidad hay dos funciones inversas.

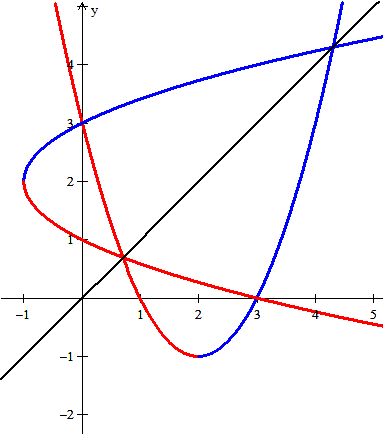
$$\begin{align}&\text {f(x) en }(-\infty,2]\implies f^{-1}(x)=2-\sqrt{1+x}\\ &\\ &\text {f(x) en }[2,\infty)\implies f^{-1}(x)=2+\sqrt{1-x}\end{align}$$

El dibujo muestra la simetría respecto de la recta y=x de las respectivas funciones inversas y su trozo de la original, lo cual significa que está bien, Aunque lo mejor es comprobarlo analíticamente

$$\begin{align}&f[f^{-1}(x)]=(2+\sqrt{1+x})^2-4(2+\sqrt{1-x})+3 =\\ &4 + 4 \sqrt{1+x}+1+x-8-4 \sqrt{1+x}+3 =\\ &4 +1+x-8+3 = x\\ &\\ &\\ &f[f^{-1}(x)]=(2-\sqrt{1+x})^2-4(2-\sqrt{1-x})+3 =\\ &4 - 4 \sqrt{1+x}+1+x-8+4 \sqrt{1+x}+3 =\\ &4 +1+x-8+3 = x\end{align}$$

Luego se cumple que la función compuesta con la inversa es la identidad.

Y eso es todo.