Solución ejercicio 1b pagina 344

Esta es la gráfica del dominio

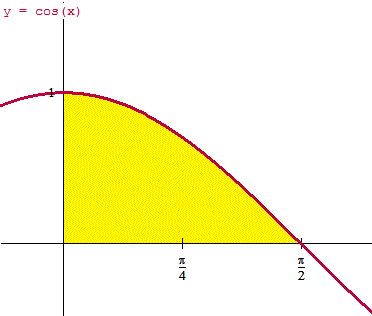
He usado variables x y y porque el programa de gráficas no admite otras, pero la y equivale a la r, y la x a theta

$$\begin{align}&\int_0^{\pi/2}\int_0^{\cos \theta}\cos \theta\; dr\; d\theta=\\ &\\ &\int_0^{\pi/2}\cos \theta·r|_0^{\cos \theta}d\theta=\\ &\\ &\int_0^{\pi/2}\cos^2\theta\, d\theta=\\ &\\ &\int_0^{\pi/2}\left(\frac{1-\cos 2\theta}{2}  \right)d\theta=\\ &\\ &\left[\frac {\theta}{2}-\frac{sen \,2\theta}{4}  \right]_0^{\pi/2}=\\ &\\ &\\ &\frac{\pi}{4}-0-0+0=\frac{\pi}{4}\end{align}$$

Para cambiar el orden de integración debemos hacer fijos los límites de la variable r y poner los de la theta como una función de r.

r toma valores entre 0 y 1

y si antes teníamos la función

r=cos(theta)

ahora será

theta = arcos(r)

Con ello la integral será

$$\begin{align}&\int_0^1\int_0^{arcos(r)}\cos\theta\; d\theta\, dr=\\ &\\ &\int_0^1[sen\theta]_0^{arcos(r)}dr=\\ &\\ &\int_0^1sen(arcos(r))dr=\\ &\\ &\text{Si }\cos \theta=r\implies sen \theta= \sqrt{1-r^2}\\ &\\ &=\int_0^1 \sqrt{1-r^2}dr=\\ &\\ &r=sen\,t  \quad dr= \cos t \,dt\\ &t=arcsen(r)\\ &r=0\implies t=0\\ &r=1\implies t=\pi/2\\ &\\ &=\int_0^{\pi/2} \sqrt{1-sen^2t}\cos t\,dt=\\ &\\ &\int_0^{\pi/2}\cos^2t\,dt\end{align}$$

Y no es necesario que continuemos porque si te das cuanta hemos llegado a la misma integral que llegamos antes, aunque la variable tenga otro nombre el resultado es el mismo, luego la terminación de esta parte es igual que la terminación de la anterior.

Y eso es todo.