Calculo Tangente a curva

La recta tangente a f(x) en (xo, yo) tiene ecuación
y = yo + f '(xo)(x-xo)
Calculamos primero la tangente en x=1
f(1) = 1-2 = -1
f '(x) = 3x^2 - 2
f '(1) = 3-1=1
Luego la recta tangente en x=1 es
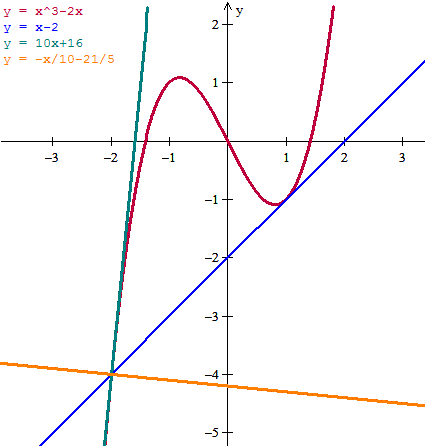
y = -1 + 1(x-1) = x-2
Y la otra intersección con la curva es
x^3-2x = x-2
x^3 - 3x + 2 = 0
Probamos con los divisores del último término {1, -1, 2, -2}
Con x=1 no es necesario, ya sabemos que lo cumple porque la recta es tangente a la curva
Con x=-1
-1 +3+2 = 4
Con x=2
8 - 6 + 2 = 4
con x=-2
-8 + 6 + 2 = 0
Este sí lo cumple, el punto de intersección tiene coordenada x=-2
y= (-2)^3 -2(-2) = -8+4 = -4
Luego el otro punto de intersección es
(-2, -4)
Recuerdo que la derivada era
f'(x) = 3x^2 - 2
f'(-2) = 12-2 = 10
La recta tangente en (-2,4) será
y = -4 + 10(x+2)
y = 10x + 16
Y la recta normal tiene ecuación
y = yo - [1/f(xo)](x-xo)
y = -4 - (1/10)(x+2)
y = -x/10 - 42/10
y= -x/10 - 21/5

Y eso es todo.