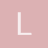Tenemos que usar una formula o producto notable menos conocido que dice:
a^3 + b^3 = (a+b)(a^2 + b^2 - ab)
Puede comprobarse que es verdadera
(a+b)(a^2 + b^2 - ab) = a^3 + ab^2 - a^2·b +a^2·b + b^3 - ab^2 = a^3 + b^3
Aplicado a lo que tenemos sería
$$\begin{align}&x^3 +\frac{1}{x^3}=\left(x +\frac 1x \right)\left(x^2+\frac{1}{x^2}-1 \right)=\\ &\\ &\sqrt 7\left(x^2+\frac{1}{x^2}-1 \right)=\\ &\\ &\text {Ahora comprobamos cuánto vale esto}\\ &\\ &\left(x+ \frac 1x \right)^2 =x^2+\frac{1}{x^2}+2\\ &\\ &\text{Esto es 3 más que el factor de arriba}\\ &\text{Como esto es 7, el factor de arriba es 4}\\ &\\ &\text{Luego el resultado final es:}\\ &\\ &=4 \sqrt 7\end{align}$$ Y eso es todo.