Sólidos de Revolución (Segunda parte) garantía de 5

Los ejes de giro son rectas verticales paralelas al eje Y. Lo que haremos serán unos cambios de variable que transformen las rectas x=4 o x=6 en el eje Y y entonces calcularemos los volúmenes con las integrales propias para volúmenes de funciones que giran en torno al eje Y.

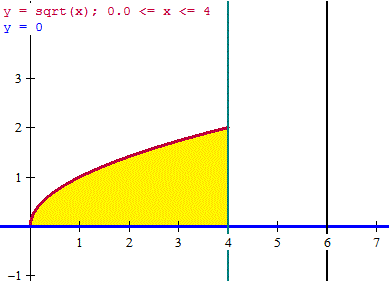
En amarillo está la superficie que genera el volumen al girar

c)

Para que la recta x=4 sea el eje Y hacemos la traslación x=z+4

Como puedes ver x=0 se corresponderá con z=-4 y x=4 se corresponderá con z=0 siendo el nuevo eje Y

La función quedará asi

y = sqrt(z+4)

Como va a girar respecto del nuevo eje y tenemos que poner z como función de y para el cálculo de la integral

y^2 = z+4

z= y^2-4

y los límites de integración en y son 0 y 2

$$\begin{align}&V=\pi\int_0^2(y^2-4)^2dy=\\ &\\ &\pi\int_0^2(y^4-8y^2+16)dy=\\ &\\ &\pi\left[\frac{y^5}{5}-\frac{8y^3}{3}+16y  \right]_0^2=\\ &\\ &\pi\left(\frac{32}{5}-\frac{64}{3}+32  \right)=\\ &\\ &\pi\left(\frac{96-320+480}{15}  \right)=\\ &\\ &\\ &\frac{256}{15}\pi\end{align}$$

d) Para que la recta x=6 sea el eje Y hacemos el cambio x=z+6

y=sqrt(z+6)

y^2 = z+6

z = y^2-6

Esta función nos va a dar el volumen total pero el sólido es como un donut, tendremos que quitarle el volumen por la recta x=4 que se transforma en

z+6=4

z=-2

Con todo esto el volumen es:

$$\begin{align}&V=\pi\int_0^2(y^2-6)^2dy-\pi\int_0^2(-2)^2dy=\\ &\\ &\\ &\pi\int_0^2(y^4-12y^2+36 - 4)dy=\\ &\\ &\\ &\pi\int_0^2(y^4-12y^2+32)dy=\\ &\\ &\\ &\pi\left[\frac{y^5}{5}-4y^3+32y  \right]_0^2=\\ &\\ &\\ &\pi\left(\frac{32}{5}-32+64  \right)=\\ &\\ &\\ &\pi\left(\frac{32}{5}+32  \right)=\\ &\\ &\\ &\frac{192}{5}\pi\end{align}$$

Y eso es todo.