Hallar la derivada
TENIENDO EN CUENTA EL EJEMPLO DICHO EN LAS ANTERIORES PREGUNTAS
Hallar la ecuación de la recta tangente de la gráfica f en el punto
indicado y comprobar la repuesta dibujando la gráfica de f y la recta obtenida
FUNCIÓN:
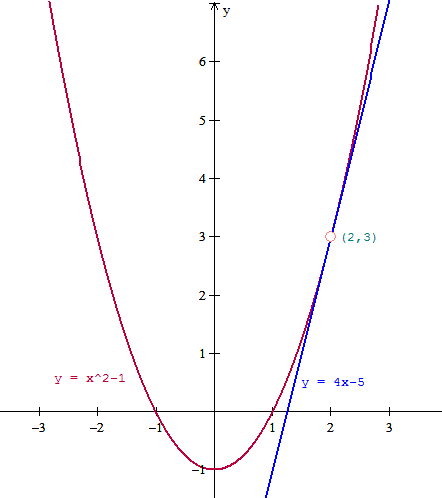
$$f(x)=x^2-1$$
PUNTO DE TANGENCIA:
(2,3)
Muchisimas gracias; la ayuda ha sido de gran apoyo
1 respuesta
Respuesta de Valero Angel Serrano Mercadal
1
Calculamos la derivada en (2, 3) por definición
$$\begin{align}&f'(2) = \lim_{h \to 0} \frac{(2+h)^2-1 -(2^2-1)}{h}=\\ &\\ &\lim_{h\to 0}\frac{4+4h+h^2-1-4+1}{h}=\\ &\\ &\lim_{h \to 0} \frac{h^2+4h}{h}=\lim_{h\to 0}(h+4)=4\end{align}$$Y ahora usamos la fórmula de la recta tangente en (xo,yo)
y = yo + f '(xo)(x-xo)
y = 3 + 4(x-2)
y = 3 + 4x -8
y = 4x - 5
Y la gráfica es esta
Y eso es todo.
