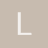Tamaño de la muestra para población infinita
Estoy realizando un proyecto para residenciarme de Ing. Industrial, el proyecto lo estoy realizando en una industria dedicada a la fabricación de papel y éste consiste en disminuir el desperdicio que es generado por el equipo que maneja las bobinas de papel, (Las bobinas de papel son la forma del producto semielaborado), este desperdicio no se encuentra calculado, por lo que si hago mejoras para la disminución de este desperdicio, necesito tener cuanto es el desperdicio actual para compararlo con el desperdicio que se obtiene con las mejoras. Considero que la población es infinita porque la producción de bobinas de papel es constante, los 7 días de la semana las 24 horas del día.
Encontré una fórmula para el calculo del tamaño de la muestra de una población infinita, pero existe un dato "P" = Prevalencia esperada del parámetro a evaluar en caso de desconcerse se aplica la opción más desfavorable 0.5.
Nota: De la población no se conoce ningún parámetro.
Entonces, Necesito saber si para mi caso esta fórmula aplica y de ser así el dato "P" que significa para mi caso.
De no aplicar esta fórmula, que fórmula podría utilizar.
Cualquier cosa adicional que necesite saber puede comunicarse conmigo a través de esta vía.
Encontré una fórmula para el calculo del tamaño de la muestra de una población infinita, pero existe un dato "P" = Prevalencia esperada del parámetro a evaluar en caso de desconcerse se aplica la opción más desfavorable 0.5.
Nota: De la población no se conoce ningún parámetro.
Entonces, Necesito saber si para mi caso esta fórmula aplica y de ser así el dato "P" que significa para mi caso.
De no aplicar esta fórmula, que fórmula podría utilizar.
Cualquier cosa adicional que necesite saber puede comunicarse conmigo a través de esta vía.
1 respuesta
Respuesta de therion_bcn
1
¿Qué quieres controlar, la calidad de las bobinas o la calidad del papel? Y luego ¿qué variables quieres controlar, diámetro, gramaje, brillo, etc...?.
Saludos, yo solo quiero calcular el desperdicio promedio por bobina generado por el método actual de manejo de las bobinas.
Para luego mediante un análisis de las causas que generan maltrato a las bobinas formular mejoras para el sistema de manejo actual.
Necesito saber cuanto son los KG. de desperdicio promedio por bobina para que luego de implantadas las mejoras poder comparar el promedio de desperdicio luego de implantadas las mejoras contra el promedio de desperdicio antes de haber realizado dichas mejoras.
Gracias.
De nuevo cualquier duda hacérmelas llegar por este medio.
Para luego mediante un análisis de las causas que generan maltrato a las bobinas formular mejoras para el sistema de manejo actual.
Necesito saber cuanto son los KG. de desperdicio promedio por bobina para que luego de implantadas las mejoras poder comparar el promedio de desperdicio luego de implantadas las mejoras contra el promedio de desperdicio antes de haber realizado dichas mejoras.
Gracias.
De nuevo cualquier duda hacérmelas llegar por este medio.
Muchas gracias me ha sidi de gran utilidad
Primero perdona por la tardanza, pero he tenido ciertos problemas con el correo.
Respondiendo a tu pregunta, la fórmula que quieres es la siguiente:
n=(K·P·Q)/(error estadístico)^2
Donde:
n: Muestra
K: número de sigmas (o desviaciones) según una distribución Normal(0,1). Usualmente K=2, es decir 2 sigmas, que representan el 95.94% de la distribución, según: P[media ? 2sigmas <= X <= media + 2sigmas] = P[-2 <= N(0, 1) <= 2] = F(2) ? F(-2) = 2 FN(0,1) (2) ? 1 = 95.94 % tal que F(X) sigue una N(0,1).
P: es la probabilidad de incertidumbre, tal que P+Q=1. Si se usa P=Q=0.5 es por desconocimiento de la probabilidad de que ocurra un suceso aleatorio, así que se utiliza la máxima incertidumbre (P=0.5).
Error estadístico: es el error estadístico que se quiere. Normalmente a un nivel de significación del 95%, es del 5%.
Así, si K=2, P=Q=0.5 i error estadístico es 0.05, obtenemos que n=400.
Yo el tratamiento que usaría, sería el de realizar 4 ó 5 extracciones aleatorias cada cuarto de hora (más o menos, 16 ó 20 por hora) y realizar un gráfico X-R, para observar derivas. Más o menos dependiendo de cada opción se realiza entre 320 extracciones (5.6% de error estadístico) y 480 extracciones (4.6% de error estadístico), que te sirve para hacer el cálculo diario.
Otra buena opción sería realizar un estudio preliminar de capacidad de máquina, es decir, coger aproximadamente 100 unidades y realizar un test de normalidad de Kolmogorov-Smirnov o un ajuste visual con un gráfico de dispersión (detección de valores extremos).
Respondiendo a tu pregunta, la fórmula que quieres es la siguiente:
n=(K·P·Q)/(error estadístico)^2
Donde:
n: Muestra
K: número de sigmas (o desviaciones) según una distribución Normal(0,1). Usualmente K=2, es decir 2 sigmas, que representan el 95.94% de la distribución, según: P[media ? 2sigmas <= X <= media + 2sigmas] = P[-2 <= N(0, 1) <= 2] = F(2) ? F(-2) = 2 FN(0,1) (2) ? 1 = 95.94 % tal que F(X) sigue una N(0,1).
P: es la probabilidad de incertidumbre, tal que P+Q=1. Si se usa P=Q=0.5 es por desconocimiento de la probabilidad de que ocurra un suceso aleatorio, así que se utiliza la máxima incertidumbre (P=0.5).
Error estadístico: es el error estadístico que se quiere. Normalmente a un nivel de significación del 95%, es del 5%.
Así, si K=2, P=Q=0.5 i error estadístico es 0.05, obtenemos que n=400.
Yo el tratamiento que usaría, sería el de realizar 4 ó 5 extracciones aleatorias cada cuarto de hora (más o menos, 16 ó 20 por hora) y realizar un gráfico X-R, para observar derivas. Más o menos dependiendo de cada opción se realiza entre 320 extracciones (5.6% de error estadístico) y 480 extracciones (4.6% de error estadístico), que te sirve para hacer el cálculo diario.
Otra buena opción sería realizar un estudio preliminar de capacidad de máquina, es decir, coger aproximadamente 100 unidades y realizar un test de normalidad de Kolmogorov-Smirnov o un ajuste visual con un gráfico de dispersión (detección de valores extremos).
