Ayudenme por favor este ejercicio de DINAMICA ... Gracias

Según justificado en problema anterior (aplicando derivación e integración)...

      a) la posición es            x = 2'5 t^2 - 0'5 t^3 +5

      b) la velocidad es (derivando)..           .v =. 5t -1'5.t^2

      c) para t=3... se sustituye en la ec. anterior , dando como resultado.. x = 14m ,,, v = 1'5 m/s

           como acelerac. = derivada v... a = 5-3.t   ---->  a = - 4 m/s^2

d) Para t=8 se reitera como antes.. y el espacio recorrido entre t3 y t8 es la diferencia:

          x8 = -105m       v8 =   -56 m/s,     

Saludos

Enrique Et!

Haré 1, son muchas preguntas y encima hay que hacer gráficas.

a y b)

a(t) = 5 - 3t  m/s^2

x(0)=5

v(0)=0

La velocidad es la integral de la aceleración respecto del tiempo

$$\begin{align}&v(t) = \int (5-3t)dt= 5t-\frac 32t^2 +C\\ &    \\ &    v(0)=0\implies5·0-\frac 320^2+C=0\\ &    \\ &    0-0+C=0\\ &    \\ &    C=0\\ &    \\ &    \text {luego}\\ &    \\ &    v(t)=5t-\frac 32t^2\quad m/s\end{align}$$

Y el espacio es la integral de la velocidad respecto del tiempo

$$\begin{align}&x(t)=\int\left(5t-\frac 32t^2\right)dt=\\ &  \\ &  \frac 52t^2-\frac 36t^3+C=\frac 52t^2-\frac 12t^3+C\\ &  \\ &  x(0)=5\implies0-0+C=5\implies C=5\\ &  \\ &  x(t) = \frac 52t^2-\frac 12t^3+5\quad m\end{align}$$

c)  En el punto t = 3s tendremos

a(3) = 5 - 3·3 = 5-9 = -4 m/s^2

v(3) = 5·3 - (3/2)3^2 = 15 - (3/2)·9 = 15 - 27/2 = 3/2 m/s

x(3) = (5/2)3^2 - (1/2)3^3 + 5 = 45/2 - 27/2 + 5 = 18/2 + 5 = 14 m

d) Ya hemos calculado el espacio recorrido a los 3 segundos, calculemos el espacio recorrido a los 8

x(8) = (5/2)8^2 - (1/2)8^3 + 5 = 320/2 - 512/2 + 5 =

160 - 256 + 5 = -91

El espacio recorrido es

x(8)-x(3) = -91 - 14 = - 105 m

Entiéndase esto como está 105 metros más a la izquierda.

e)

Esta es la gráfica

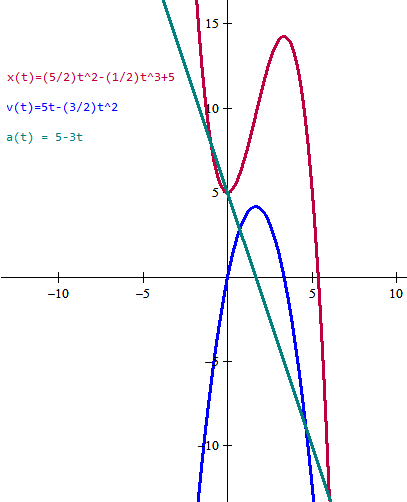
Y eso es todo, espero que te sirva y lo hayas entendido. Son ejercicios con mucho trabajo, uno por pregunta.