¿Cómo puedo graficar la derivada de la función f(x)=senx en Geogebra?
Hola Valero
Finalmente pude valorar la respuesta anterior, iba comentar para poder seguir pero no se pudo, no sé que pasa, pero bueno. Tengo un problema en Geogebra, donde yo gráfico la función f(x) = senx directamente, y la maestra quiere que obtengamos la derivada de esa función trazando una recta tangente y una perpendicular, y luego moviéndola nos dará la derivada que es la gráfica de la función g(x) = cosx, pero es que no le entendí muy bien la verdad. No sé si usted sepa algo de esto, sino, toca investigar.
Espero su ayuda. Gracias de antemano.
No conozco yo ese método tan ingenioso para calcular la derivada ni lo he visto hacer, tendrías que darme más detalles.
Bueno, lo primero para hacer la gráfica de la función seno escribes por ejemplo
f=Curva(t, sen(t), t, 0, 2*pi)
Los dos primeros son los puntos (x, y) de la gráfica
T es el nombre del parámetro, creo qyue debe ser t, le puse x y no funcionaba
0 y 2*pi son los límites del parámetro. Si quieres más o menos dominio puedes cambiarlos.
Dibujando la tangente en un punto t0 de la gráfica con la herramienta Tangentes del menú tendremos una recta cuya pendiente es
Cos(t0)
Si le trazamos la perpendicular tendremos una recta cuya pendiente es
-1/cos(t0)
si hacemos que esa perpendicular pase por el punto (0,1) la recta va a ser
y = -[1/cos(t0)]x + 1
y el corte con el eje X va a ser
0 = -[1/cos(t0)]x + 1
-1 = -[1/cos(t0)] x
1 = [1/cos(t0)] x
x = 1/[1/cos(t0)] = cos(t0)
Luego el segmento entre 0 y el corte de la perpendicular pasando por (0,1) con el eje X es la medida de cos(t0), ¿Pero cómo hacemos para transportar esa medida y ponerla en vertical sobre el punto (t0, 0)?
No sé si es esto lo que ha hecho la maestra o seguramente a hecho otra cosa mejor mejor, si no me lo puedes explicar bien o darme la teoría puedo pegarme días pensando en que ha hecho sin llegar a saberlo.
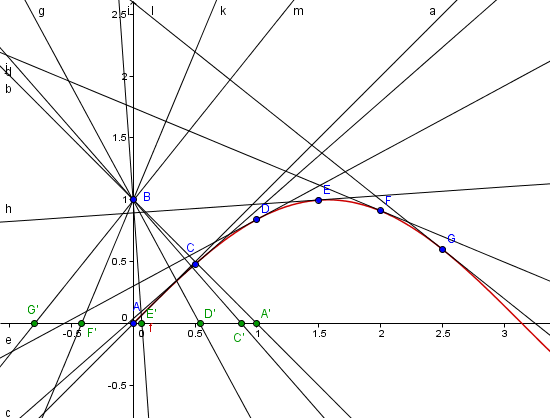
Aqui tome los puntos
A=(0,sen(0))
B=(0,1) Por donde pasan todas las perpendiculares
C=(0.5, sen(0,5)
D=(1,sen(1))
E=(1.5, sen(1,5))
...
Trace la tangente por cada uno y luego la perpendicular pasando por (0,1) y luego el corte de esa perperdicular con el eje X dándome los puntos A', B', C', ...
Que son el valor respectivo del coseno para 0, 0.5, 1, 1.5, ...
Pero que no sé como se continuaría o si no merece la pena continuar desde aquí sino hacerlo de otra forma.
Hola, muchas gracias por su tiempo dedicado, la verdad es que ha sido mucho lo que ha escrito. Pero ya sé en este momento como poder graficar la derivada de Seno, incluso de más funciones, aunque no creo que de todas.
Le mandaré en este momento un correo donde le adjunto el trabajo por si le interesa analizarlo.
Saludos
Yo ya pensaba que tendría que ser mucho más sencillo. Pero el enunciado me confundió, como hablabas de una perpendicular yo pensaba que era perpendicular a la tangente y de esa forma ya ves el churro que sale. Tambén estaba buscando un método que te dibujase la curva como fruto de algunas intersecciones, pero vista la respuesta tienes que hacer a mano los traslados de segmentos para dibujarla, es poco más o menos lo mismo que en la mía, solo que en la mía aparte hay que girar 90 grados los segmentos.
Y estuve pensando en algo así, pero lo de la perpendicular me engañaba.
E verdad confunde por completo - Kariime ÁlvArezz