Ejercicios de máximos y mínimos, matemáticas aplicada
Sea , f(x) =–x (elevado a la 2) + 8x -24
encuentre lo siguiente:
- Valores máximos ó mínimos.
- Intercepto con los ejes
- Graficar la función.
1 Respuesta
Respuesta de Valero Angel Serrano Mercadal
Lucha p.v!
·
1)
Para hallar los máximos o mínimos se deriva la función y se iguala a 0
f '(x) = -2x + 8 = 0
-2x=-8
x=4
Sabemos que es un parábola hacia abajo y por eso es un máximo. Pero podemos usar el método general, calculando la derivada segunda
f ''(x) = -2
f ''(4) = -2
Como la derivada segunda en ese punto es negativa es un máximo.
f(4) = -4^2 +8·4 - 24 = -16 + 32 - 24 = -8
Luego el punto (4, -8) es el máximo
·
2)
La intersección con el eje Y es la mas sencilla, se da cuando x=0
f(0) = -0^2 +8·0 - 24 = -24
Y la intersección con el eje X se da cuando y=0
-x^2 + 8x - 24 = 0
x^2 - 8x + 24 = 0
$$\begin{align}&x=\frac{8\pm \sqrt{64-96}}{2}= \frac{8\pm \sqrt{-32}}{2}\end{align}$$No corta al eje X ya que no hay soluciones reales de esa ecuación.
·
c)
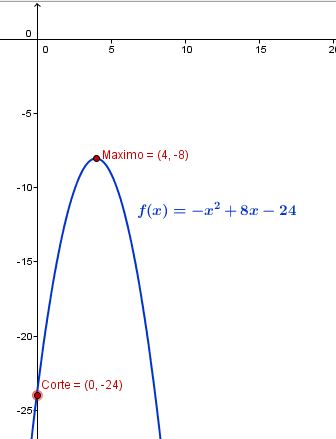
Y esta es la gráfica:
