¿Quien me puede ayudar con este ejercicio?

$$\begin{align}&f(x)=\frac{x^2-2}{ \sqrt{(x^2-4)}}\\ &\\ &Dominio: \   \ x^2-4>0   \Rightarrow(-\infty,-2)U(2,+\infty)\\ &\\ &No \ corta \ al \ eje \ OY \ x=0  \ No\ es \ del \ Dom\\ &\\ &No \ corta \ al \ eje \ OX \ y=0 \  \Rightarrow x^2-2=0 \ \Rightarrow \ x= \pm \sqrt{2}  \ No \ pertenece \ Dom\\ &\\ &Función\  Par\ , simétrica \ respecto \ OY \ f(x)=f(-x)\\ &\\ &Regionamiento: \ La \ función \ es \ siempre \ positiva \ en \ todo \ el \ Dominio\\ &\\ &\lim_{x \to\ -2^-}f(x)= \lim_{x \to\ 2^+}f(x)=\frac{2^2-2}{ \sqrt{(2^2-4)}}=\frac{2}{0}=\infty\\ &\\ &Asintotas Verticales  \ x=2   \ \  x=-2\\ &\\ &Crecimiento:\\ &f'(x)=\frac{2x \sqrt{x^2-4}-\frac{2x(x^2-2)}{2 \sqrt{x^2-4}{x}}}{x^2-4}=\frac{2x(x^2-4)-x(x^2-2)}{\sqrt{x^2-4}^3}=\\ &\\ &f'(x)=\frac{x^3-6x}{\sqrt{x^2-4}^3}=0\\ &\\ &x^3-6x=0\\ &x(x^2-6)=0\\ &x=\pm \sqrt{6}\\ &\\ &Intervalos \ de \ crecimiento :\\ &(-\infty,-\sqrt{6})f'<0\\ &(-\sqrt{6},-\sqrt{2})f'>0\\ &(2,+\sqrt{6})f'<0\\ &(+\sqrt{6},+\infty)f'>0\\ &\\ &Minimo \ relativo (-\sqrt{6} , 2 \sqrt{2})\\ &Max \ relativo (\sqrt{6} , 2 \sqrt{2})\\ &\\ &Grafica:\\ &\\ &\\ &\\ &\\ &\\ &\\ & \end{align}$$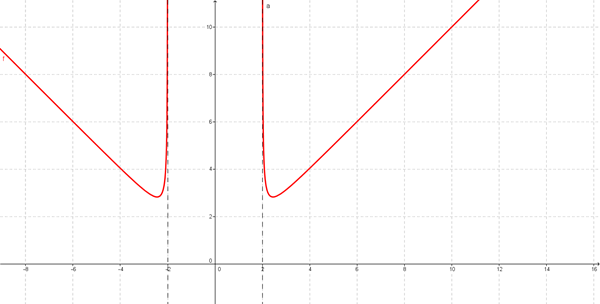

Espero que te sirva

Un saludo.

Recuerda valorar la pregunta. Es lo único que se pide en esta web,

Excelente es lo correcto